Las leyes, las leyes de potencia y la estadística: un viaje a través de la ciencia de los datos En el vasto universo de la ciencia, pocos aspectos son tan fascinantes y fundamentales como el análisis de datos. La capacidad de interpretar y comprender la información que recolectamos a través de observaciones y experimentos es esencial para el avance del conocimiento. En este contexto, las leyes y las leyes de potencia emergen como conceptos cruciales que nos permiten dar sentido a fenómenos complejos en la naturaleza. Las leyes científicas son relaciones que describen patrones observables en la realidad. Estas leyes pueden ser simples, como la ley de la gravedad de Newton, o más complejas, como la ley de conservación de la energía.
Sin embargo, existen también leyes más intrigantes, como las leyes de potencia, que desafían nuestras intuiciones y nos llevan a cuestionar cómo se distribuyen ciertos fenómenos en el universo. Uno de los ejemplos más célebres de leyes de potencia es la Ley de Gutenberg-Richter, que describe la relación entre la magnitud de los terremotos y la frecuencia con la que ocurren. Este fenómeno, estudiado por los geofísicos Beno Gutenberg y Charles Richter, establece que la probabilidad de que ocurra un terremoto de cierta magnitud disminuye de manera específica a medida que la magnitud aumenta. En términos prácticos, esto significa que mientras que los terremotos pequeños son comunes, los grandes terremotos son raros, lo que revela una falta de escalas inherentes en la distribución de estos eventos. Las leyes de potencia no solo se manifiestan en la geofísica, sino que también aparecen en diversas áreas de estudio, tales como la biología, la economía y la tecnología.
Por ejemplo, se han registrado distribuciones de leyes de potencia en la creación de redes sociales en línea, donde unos pocos usuarios generan la mayoría de los enlaces, así como en la distribución de riquezas, donde una pequeña fracción de la población controla la mayor parte de los recursos. Sin embargo, el camino hacia la validación de estas leyes no es sencillo. Un desafío importante radica en la calidad y la cantidad de los datos disponibles. Como menciona el científico Mark Buchanan en su artículo "Leyes, leyes de potencia y estadísticas", el análisis adecuado de los datos es fundamental para discernir la veracidad de las teorías. A menudo, los datos pueden ser escasos o imprecisos, lo que lleva a conclusiones erróneas o a la confirmación de creencias preexistentes.
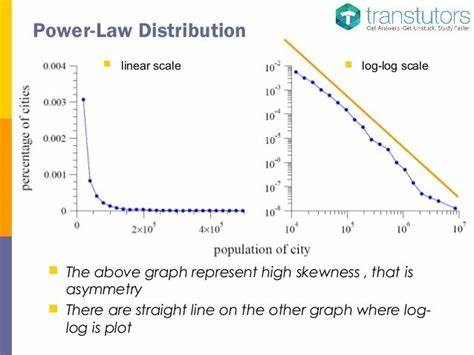
Un aspecto crucial del análisis de datos es la forma en que se procesan. La técnica más común para extraer patrones de un conjunto de datos es utilizar histogramas, que reflejan una estimación empírica de la densidad de probabilidad. Cuando se sugiere que los datos siguen una ley de potencia, la representación gráfica en un gráfico log-log debería mostrar una relación lineal. Sin embargo, el apresuramiento en aceptar como válidos estos resultados puede llevar a errores significativos. Los estudios recientes, particularmente el llevado a cabo por Aaron Clauset y sus colegas, han demostrado que el uso de regresiones lineales puede ser problemático.
Esta técnica, que se basa en el supuesto de que los errores de los datos en diferentes intervalos son independientes y distribuidos de forma gaussiana, puede ser inaplicable una vez que los datos han sido transformados logarítmicamente. Esto puede dar lugar a conclusiones incorrectas que se filtran en la literatura científica. Clauset y su equipo propusieron un enfoque más riguroso para el análisis de datos que implicaba una evaluación cuidadosa de la probabilidad de que los datos empíricos provengan realmente de una ley de potencia. En lugar de aceptar automáticamente que una distribución se ajusta a una ley de potencia, enfatizan la necesidad de comparar su bondad de ajuste con otras distribuciones posibles, como las distribuciones exponenciales o log-normales. Este rigor es esencial para evitar caer en ilusiones estadísticas que pueden distorsionar nuestra comprensión del mundo.
La necesidad de un enfoque más metódico se vuelve evidente al revisar los conjuntos de datos que se han analizado en el pasado. En su análisis, Clauset estudió 24 conjuntos de datos reales en los cuales se habían propuesto leyes de potencia previamente. Los resultados variaron, revelando que algunos, como la distribución de incendios forestales y la de enlaces en la web, mostraron un ajuste moderado a las leyes de potencia, aunque otras formas matemáticas resultaron ser más adecuadas. Por otro lado, la distribución de la riqueza no se ajustó a las leyes de potencia, lo que resalta la importancia de una evaluación exhaustiva de los datos y sus interpretaciones. En última instancia, la misión del análisis de datos en la ciencia es despojar nuestras intuiciones y deseos de la ecuación.
Como bien señala Buchanan, los métodos estadísticos son herramientas que nos dicen lo que los datos pueden o no afirmar. La emoción del descubrimiento científico puede verse empañada por la desilusión cuando los resultados no se alinean con nuestras expectativas. Sin embargo, este es precisamente el valor del trabajo riguroso en el análisis de datos: nos ayuda a combatir el pensamiento ilusorio y nos dirige hacia una comprensión más precisa del universo. En un mundo donde la información abunda, el desafío radica en cómo la analizamos y la interpretamos correctamente. Las leyes de potencia y su análisis estadístico son un recordatorio de que, en la ciencia, no podemos permitirnos caer en la trampa de la simplicidad engañosa.