La turbulencia es uno de los fenómenos más comunes que observamos en la naturaleza y en nuestra vida diaria, pero paradójicamente, sigue siendo uno de los problemas científicos más complejos y, en muchos sentidos, sin resolver en la física. A pesar de los avances significativos en matemáticas, computación y experimentación, los científicos aún luchan por desarrollar una teoría completa que describa y prediga todos los aspectos del comportamiento turbulento en fluidos como el agua y el aire. Este fenómeno no solo representa un desafío teórico, sino que también tiene un impacto enorme en el diseño tecnológico y la comprensión de procesos naturales tan diversos como la meteorología, la aeronáutica y el transporte de líquidos en tuberías. Uno de los aspectos que hacen que la turbulencia sea tan esquiva reside en la naturaleza misma de sus movimientos: caóticos, impredecibles y extremadamente complejos. A nivel cotidiano, aunque no es posible ver el aire como un fluido en movimiento, cuando agitamos la mano o miramos el flujo de un río, estábamos acercándonos a la esencia del fenómeno turbulento.
El desafío para los científicos es cómo describir y predecir estos cambios complejos utilizando las leyes físicas conocidas, en particular las ecuaciones que gobiernan el movimiento de fluidos, donde la famosa ecuación de Navier-Stokes juega un papel central. Desde hace casi dos siglos, la ecuación de Navier-Stokes ha ofrecido la base matemática para estudiar la dinámica de fluidos. Derivada aplicando las leyes clásicas de Newton al comportamiento de fluidos, esta ecuación es la herramienta fundamental para analizar cómo se mueve el agua, el aire y otros líquidos o gases. Sin embargo, un problema crucial es que es una ecuación no lineal, lo que significa que las soluciones no se pueden construir sumando soluciones simples. Este carácter no lineal introduce una complejidad enorme y es la raíz de muchas dificultades para resolver problemas relacionados con la turbulencia.
Por ello, incluso matemáticos y físicos de la talla de Werner Heisenberg dedicaron años a estudiarla sin poder alcanzar una solución definitiva. Werner Heisenberg, conocido por sus revolucionarias contribuciones a la mecánica cuántica, describió la turbulencia como una de las dos grandes incógnitas que le gustaría preguntar a Dios, la otra siendo la naturaleza de la mecánica cuántica misma. Esto ilustra la envergadura y profundidad del misterio que implica la turbulencia. A pesar de la genialidad matemática de Heisenberg, solo logró avances parciales en su investigación sobre este tema, y su trabajo refleja cómo la turbulencia ha encontrado a menudo un muro incluso para las mentes más brillantes. Desde el tiempo de Heisenberg, se han desarrollado numerosas estrategias para comprender y abordar la turbulencia.
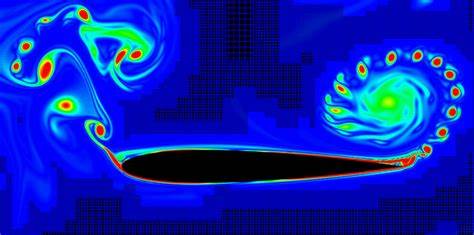
La dificultad para encontrar soluciones exactas a la ecuación de Navier-Stokes en situaciones realistas ha llevado a confiar en herramientas computacionales, popularizando el campo de la dinámica de fluidos computacional o CFD (por sus siglas en inglés). A través de la simulación numérica, los investigadores pueden aproximar comportamientos turbulentos para casos específicos, desde el flujo sobre alas de avión hasta el movimiento de fluidos en tuberías industriales. Sin embargo, estas simulaciones requieren un poder computacional colosal y solo pueden estudiar casos particulares, sin ofrecer una comprensión unificada de la turbulencia en general. Una ventaja importante de las técnicas computacionales es la posibilidad de emplear mallas adaptativas que concentran los cálculos en áreas donde el flujo es más complejo, como en los alrededores de un objeto o en zonas donde se generan vórtices y remolinos. Además, los modelos estadísticos basados en grandes turbulencias como la simulación de grandes remolinos (LES) permiten simplificar el cálculo al modelar las escalas pequeñas del flujo, que disipan energía y tienen menor efecto en la dinámica global.
Así, estas herramientas facilitan avances en la predicción de la transición de un flujo laminar, ordenado y suave, hacia un flujo turbulento, caótico y complejamente estructurado. Otra dimensión del problema es que incluso la definición precisa de qué es la turbulencia no es unánimemente aceptada. Aunque generalmente se describe como un movimiento caótico y desordenado de un fluido, para los científicos resulta difícil formalizar esta definición debido a la variedad de comportamientos y escalas temporales y espaciales que exhibe. Históricamente, figuras como Leonardo da Vinci ya intentaron analizar y representar visualmente estos patrones turbulentos hace más de 500 años. Sus dibujos de remolinos y flujos mostraban un interés sistemático por la naturaleza compleja de los fluidos y marcaban el inicio de una tradición científica y artística que continúa hasta hoy.
En la física moderna, una teoría completa de turbulencia debería ser capaz de predecir, a partir de las condiciones iniciales y las propiedades físicas del fluido, cómo se comportará el flujo en cualquier momento y lugar. Pero quienes investigan el tema enfrentan motivos que van más allá de los retos matemáticos o computacionales: la turbulencia exhibe una riqueza de fenómenos misteriosos, incluyendo transiciones repentinas de comportamiento organizado a caos, estructuras persistentes dentro de un fluido extremadamente agitado e incluso la coexistencia de zonas turbulentas con zonas laminares en un mismo flujo. Estas características complejas se observan tanto en experimentos controlados, como en la escala natural, por ejemplo, en las formaciones de tormentas gigantes en la atmósfera de Júpiter que se mantienen estables durante años, o en las olas que rompen en la orilla del mar. En estos casos, las estructuras dentro del flujo turbulento crean patrones que desafían las simples nociones de caos absoluto y apuntan a fenómenos organizados en medio de la desorganización. Uno de los enfoques teóricos que se utiliza para tratar la turbulencia es la teoría de estabilidad.
Esta rama estudia cómo un flujo ordenado pierde su estabilidad cuando se incrementan ciertas variables, como velocidad o presión, y cómo entonces emergen patrones más complejos que eventualmente derivan en turbulencia. Sin embargo, encontrar con exactitud las condiciones de transición y los mecanismos involucrados sigue siendo un objetivo en investigación y no una conclusión establecida. Los experimentos para observar los detalles de la transición entre flujos laminare y turbulentos son complejos debido a la delicadeza de los parámetros involucrados. No obstante, técnicas modernas de visualización y medición permiten seguir el desarrollo de estas transiciones en condiciones controladas, como en el estudio del flujo alrededor de cilindros o en las capas límite cercanas a paredes. Estos experimentos complementan la investigación teórica y computacional, y demuestran por qué la turbulencia representa un problema interdisciplinario que requiere colaboración entre matemáticos, físicos, ingenieros y científicos computacionales.
A nivel matemático, un problema fundamental permanece abierto: las ecuaciones de Navier-Stokes no solo son difíciles de resolver, sino que no está probada la existencia o unicidad de sus soluciones generales para todas las condiciones posibles. La resolución de esta cuestión representa uno de los siete problemas del milenio y conlleva un premio de un millón de dólares, lo que evidencia la importancia y dificultad que tiene abordar la turbulencia desde el ámbito puramente matemático. En este marco de desafíos, algunos científicos han explorado teorías que introducen aspectos de la física cuántica para explicar ciertas características de la turbulencia. A pesar de ser una postura minoritaria, esta propuesta demuestra que el estudio de la turbulencia sigue abierto a nuevas ideas y enfoques, algunos de ellos muy innovadores y aún no totalmente aceptados. La importancia práctica de comprender la turbulencia se refleja en áreas críticas de la tecnología y la industria.
La aerodinámica, fundamental para la aviación y el transporte, depende de modelos fiables de flujo turbulento para optimizar el consumo y la seguridad. En tuberías industriales, predecir con exactitud la resistencia debida a la turbulencia puede mejorar la eficiencia y reducir costos. En climatología, los modelos meteorológicos necesitan incorporar el comportamiento turbulento para mejorar la predicción del tiempo y los fenómenos extremos. A pesar de estos enormes retos, la búsqueda por entender la turbulencia ha sido una fuente constante de innovación y desarrollo científico y tecnológico. Desde los primeros dibujos de Leonardo da Vinci hasta las simulaciones en supercomputadoras modernas, cada etapa refleja un acercamiento más profundo y sofisticado a un fenómeno que, en última instancia, muestra hasta qué punto aún queda misterioso el mundo natural que nos rodea.
El problema de la turbulencia también es un recordatorio poderoso de que incluso fenómenos naturales aparentemente simples, como el flujo de agua en una tubería, pueden esconder complejidades tan profundas que superan el conocimiento científico actual. Mientras la física moderna avanza en muchos frentes, la turbulencia continúa siendo un desafío abierto, insinuando que la exploración y el descubrimiento en la ciencia no terminarán pronto. Por tanto, la turbulencia no solo es un obstáculo científico, sino también una invitación fascinante a seguir explorando los límites del conocimiento humano, a desarrollar nuevas matemáticas, tecnologías de simulación y experimentos, y a mantener viva la curiosidad por comprender cómo funciona realmente el universo a nuestro alrededor.