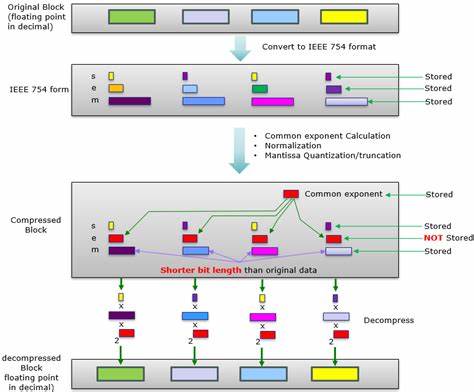
La compresión de datos numéricos, especialmente aquellos expresados en formato de punto flotante, representa un desafío continuo en el ámbito de la informática y la ingeniería. En un mundo donde la cantidad de datos generados crece exponencialmente, encontrar formas de reducir el tamaño de almacenamiento sin perder precisión ni integridad es vital para mejorar la velocidad, eficiencia y costos asociados a su transferencia y procesamiento. La pregunta crucial aquí es: ¿hasta qué punto podemos comprimir los datos en punto flotante sin comprometer su utilidad? Para responderla, debemos adentrarnos en la estructura, características y comportamiento de estos números, así como en técnicas modernas de compresión que pueden aprovechar patrones inherentes en los datos matemáticos que generamos, como los resultados de funciones trigonométricas o exponenciales. Los números en punto flotante son una representación estandarizada diseñada para codificar una amplia gama de valores numéricos que podrían ser demasiado grandes o pequeños para ser representados por enteros convencionales. En particular, las implementaciones comunes como el formato IEEE 754 definen formatos de 32 y 64 bits para almacenar números en precisión única y doble respectivamente.
Sin embargo, la densidad de información que contienen varía en función de sus componentes: el signo, la mantisa y el exponente. Este diseño permite equilibrar alcance y precisión, pero también introduce patrones que pueden ser explotados para una compresión más eficiente. El problema surge cuando queremos almacenar o transferir un conjunto masivo de resultados de cálculos matemáticos con punto flotante, por ejemplo todos los posibles resultados de la función coseno para cada número de 32 bits. Esto implica una cantidad astronómica de datos, concretamente más de cuatro mil millones de valores, lo que en bruto se traduce aproximadamente en 16 gigabytes. Aunque hoy día existen soluciones avanzadas de compresión general, como Zstandard (ZSTD), que pueden reducir estas matrices en alrededor de cinco veces en tamaño, aún estamos hablando de gigabytes de datos complejos que son difíciles y costosos de manejar, especialmente cuando la comunicación entre plataformas o dispositivos está en juego.
La clave para mejorar la compresión va más allá de un simple algoritmo; requiere entender cómo se comportan los datos que intentamos comprimir. Por ejemplo, en el caso de la función coseno, los valores generados tienden a variar lentamente y sus resultados están estrechamente relacionados en rangos específicos, especialmente dentro del dominio [-1, 1] donde más de la mitad de los valores de entrada residen. Esta continuidad relativa genera diferencias pequeñas entre números consecutivos, que deberían facilitar la compresión al aprovechar la redundancia espacial y temporal de los datos. Uno de los enfoques examinados consiste en aplicar técnicas como la codificación por diferencia (delta encoding). Esta técnica consiste en almacenar no el valor completo de cada número sino la diferencia que tiene con respecto al número anterior, lo cual puede reducir el tamaño si las diferencias son pequeñas y repetitivas.
Sin embargo, cuando la función presenta cambios drásticos como cambios de signo frecuentes, que ocurre aproximadamente el 20% de las veces en la señal coseno, estas diferencias pueden ser grandes y generar incrementos en el tamaño de almacenamiento, perdiendo efectividad. Otra técnica investigada es el uso de operaciones lógicas como XOR entre números consecutivos para tratar de resaltar cambios sutiles y eliminar patrones persistentes, facilitando así que el algoritmo de compresión posterior pueda trabajar mejor. Aunque se obtuvieron mejoras moderadas, los resultados parecían estancarse en un tamaño que todavía resultaba demasiado grande para el propósito deseado, ilustrando que sin un entendimiento más profundo o un enfoque innovador, las ganancias serán limitadas. Se exploró además la codificación variable de enteros (varint), especialmente aplicada a la mantisa tras realizar transformaciones como diferencias o XOR. Esta técnica es conocida por aprovechar el tamaño variable de la representación cuando los números son pequeños o cercanos a cero, lo que es frecuente en las diferencias entre mantisas.
Sin embargo, la variabilidad y las irregularidades presentes en la función coseno en su dominio completo dificultaron que esta técnica alcance una compresión significativa sin sacrificar compatibilidad o la necesidad de algoritmos complejos para decodificación. Cabe destacar que estos ejercicios no solo son teóricos sino que reflejan retos reales en áreas que requieren validación exhaustiva de cálculos matemáticos, como en la verificación de funciones de librerías matemáticas o en la comparación de implementaciones de distintos fabricantes. En un mundo ideal, tener la capacidad para transmitir tablas de resultados sin pérdida y en tamaños manejables entre plataformas permitiría validar resultados con una precisión insuperable, detectando discrepancias sutiles que podrían afectar aplicaciones críticas. La realidad actual pone en evidencia las limitaciones de la tecnología y la necesidad de seguir buscando nuevas alternativas. Una buena dirección para avanzar podría ser la adopción de formatos especializados para datos numéricos, como los desarrollados en ámbitos científicos y de compresión numérica que aplican técnicas estadísticas y de predictibilidad más avanzadas.
Por ejemplo, fpzip es una herramienta indicada para la compresión eficiente de datos de punto flotante multidimensional, que puede aprovechar correlaciones internas de los datos sin perder precisión significativa. También es pertinente considerar que no siempre la compresión debe ser completamente sin pérdida; existen escenarios donde distorsiones mínimas controladas pueden ser aceptables si se logran fuertes reducciones en el tamaño de datos. En este sentido, enfoques basados en compresión con pérdida para datos numéricos, siempre bajo estrictos controles de error, podrían facilitar la gestión de grandes conjuntos de resultados sin comprometer la aplicabilidad ni la confianza en ellos. Desde una perspectiva más amplia, el desafío de la compresión efectiva de datos en punto flotante invita a la colaboración de expertos en matemáticas, compresión, arquitectura de computadoras y programación. El hecho de que la reducción por compresión general no sea suficiente indica que la estructuración inteligente y la codificación adaptativa de los datos son campos prometedores para futuras innovaciones.
En conclusión, aunque las técnicas actuales como ZSTD y métodos como delta encoding o XOR proporcionan mejoras significativas con respecto a almacenar datos en crudo, los tamaños resultantes aún son demasiado grandes para ciertas aplicaciones prácticas, especialmente en el contexto de transmitir tablas completas de resultados matemáticos para verificaciones entre distintas plataformas. Explorar herramientas especializadas, aprovechar las propiedades matemáticas de los datos y aceptar compromisos calculados entre precisión y tamaño podrían ser la clave para desbloquear la compresión eficiente de punto flotante en el futuro cercano. Mientras tanto, la compresión de datos numéricos precisos continúa siendo un área activa y fascinante de investigación tecnológica.