El Juego Real de Ur, una antigua joya del mundo de los juegos de mesa, ha cautivado a jugadores y estudiosos por siglos. Sin embargo, no fue sino hasta hace poco que, gracias a avances significativos en inteligencia artificial (IA) y matemáticas, se logró resolver completamente este juego, estableciendo estrategias óptimas para cada posición y situación posible. Esta solución representa un verdadero avance en la forma en que entendemos y abordamos juegos con elementos de azar y movimientos estratégicos complejos. Resolver un juego quiere decir encontrar una estrategia perfecta que maximice las probabilidades de victoria para un jugador, asumiendo que ambos participantes juegan de forma óptima. El Juego Real de Ur presenta un reto particular para esta tarea debido a la presencia de dados, lo que introduce variabilidad y hace imposible prever una secuencia exacta de movimientos ganadores por adelantado.
A diferencia de juegos como el ajedrez, donde el jugador puede planificar una estrategia clara, Ur requiere contemplar todas las variantes posibles derivadas de cada tirada, un aspecto que lo asemeja más al póker en cuanto a la gestión y evaluación de probabilidades futuras. El equipo de investigadores dedicó siete años en la aplicación y afinamiento de técnicas sofisticadas basadas en IA para abordar este desafío. La herramienta central empleada fue la iteración de valor, un método que permite calcular la probabilidad de ganar desde cualquier posición en el tablero, evaluando todos los posibles resultados futuros y escogiendo la mejor jugada en cada caso. Este método es especialmente eficiente para juegos con un número finito pero extenso de estados posibles, tal como sucede con la versión Finkel del juego, que consta aproximadamente de 276 millones de estados. La iteración de valor opera propagando el «valor» de estados de victoria y derrota hacia atrás a través de todos los posibles estados del juego.
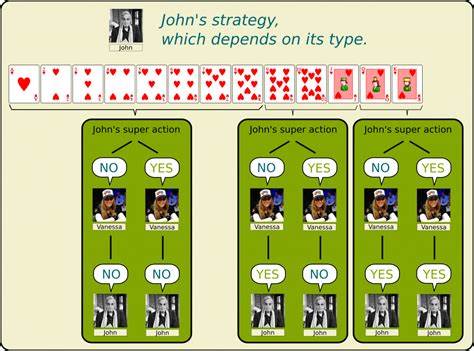
Es decir, si se conoce qué tan favorable es un estado tras una determinada jugada, se puede calcular qué tan favorable es el estado actual. Esta información se ajusta repetidamente, respetando la probabilidad de cada resultado del dado y la mejor jugada seleccionada por cada jugador, hasta que las probabilidades convergen a valores estables y altamente precisos. Las complejidades que surgieron durante el proceso incluyen la existencia de ciclos o bucles dentro del estado del juego, donde un jugador puede regresar a un estado anterior tras una serie de movimientos, lo que dificulta una simple propagación hacia atrás. La iteración de valor sobre múltiples iteraciones resolvió esta cuestión, asegurando que las dependencias circulares fueran resueltas y que los valores finales representaran estrategias óptimas y estables. También fue fundamental asumir que ambos jugadores actúan racionalmente y eligen estrategias óptimas, lo que se denomina un equilibrio de Nash en teoría de juegos.
Este supuesto simplifica la modelación ya que no intenta predecir variaciones de comportamiento humano errático, sino estrategias que ninguna de las partes puede mejorar unilateralmente. Bajo este marco, la selección de jugadas se basa en la maximización o minimización de probabilidades de victoria, de acuerdo a qué jugador esté moviendo. La implementación técnica involucró almacenar un mapa inmenso que asigna a cada estado del juego su probabilidad de victoria bajo juego óptimo. Para manejar la vastedad de estos estados, el equipo desarrolló mapas comprimidos y altamente eficientes en memoria, codificando estados en solo 32 bits en la mayoría de los casos, lo que permitió una gestión eficiente de datos sin sacrificar precisión. Estos mapas podían comprimirse todavía más si se toleraba una mínima pérdida de exactitud.
Un elemento interesante del proceso fue la subdivisión del juego original en «mini-juegos», que simplificaron el problema eliminando ciclos mediante la segmentación basada en el puntaje obtenido. Esto permitió acelerar el cómputo al enfocarse en subconjuntos de estados relacionados, facilitando un entrenamiento iterativo más rápido y eficiente. Tal división aprovechó que una vez que una pieza anota, no puede revertir su estado, diseccionando el problema para optimizar tiempos y recursos. En términos prácticos, la solución proporciona una tabla completa de probabilidades para todas las configuraciones posibles, permitiendo crear una inteligencia artificial que juega perfectamente y que es invencible, conocida actualmente como la bot perfecta para el Juego Real de Ur. Además, esta base tiene aplicaciones educativas y analíticas; los jugadores pueden revisar partidas, medir la precisión de sus movimientos y comprender mejor las decisiones óptimas.
Este logro también ofrece una perspectiva valiosa sobre la resolución de juegos con azar y elevada complejidad. Aunque la iteración de valor se adapta muy bien a Ur debido a su espacio de estados relativamente manejable, juegos más complejos con partidas mucho más largas y mayor variedad de estados, como el backgammon, aún permanecen fuera de alcance para este método directo por sus requerimientos computacionales exorbitantes. La solución del Royal Game of Ur evidencia una simbiosis perfecta entre conocimientos matemáticos, computacionales y teóricos de juegos, marcando un hito en la investigación de IA aplicada a juegos de mesa. Además, al liberar tanto los modelos como el código fuente en plataformas abiertas, el equipo invita a la comunidad global a explorar, probar y extender este conocimiento, detonando oportunidades para crear bots más avanzados, desarrollar nuevas estrategias y mejorar la experiencia de juego. En definitiva, resolver el Juego Real de Ur ha sido un viaje apasionante, que muestra que dando con la combinación adecuada de método matemático y tecnología es posible alcanzar niveles de perfección antes inimaginables, incluso para juegos combinando estrategia y azar.
Las implicaciones van más allá del ámbito lúdico, impactando el desarrollo de sistemas de decisión bajo incertidumbre, análisis de riesgo y predicción en dominios diversos. Para quienes deseen aventurarse en el mundo de Ur o comprender en profundidad la matemática detrás, la comunidad ha dispuesto recursos, librerías en Java y Python, y visores que permiten explorar cada posición con su probabilidad optimizada. Es un momento emocionante para jugadores, desarrolladores y académicos, donde el pasado milenario de Ur se encuentra con el futuro innovador de la inteligencia artificial. Este caso también abre el debate sobre qué otros juegos podría ser posible resolver y a qué costo, ampliando la frontera del conocimiento en inteligencia artificial y teoría de juegos. Así, mientras algunos clásicos complejos aún son inconmensurables para máquinas, pequeñas maravillas como el Royal Game of Ur demuestran que no existen límites para la creatividad y perseverancia aplicada a la resolución de problemas estratégicos complejos.
En resumen, la solución del Juego Real de Ur representa una conjunción perfecta de profundidad histórica, innovación tecnológica y matemáticas aplicadas, un faro para futuros esfuerzos en la inteligencia artificial que busca dominar juegos y entornos con elementos de incertidumbre y estrategia compleja.