La esfera cornuda de Alexander representa una de las construcciones más intrigantes y desafiantes en el campo de la topología geométrica. Descubierta en 1924 por el matemático estadounidense J. W. Alexander, esta figura revela un comportamiento sorprendente y paradójico al considerar la forma en que se puede incrustar una esfera bidimensional en el espacio tridimensional. Más allá de ser una curiosidad matemática, la esfera cornuda tiene consecuencias profundas que han influido en el desarrollo de la topología, la diferenciación entre categorías de variedades, y la comprensión de conceptos fundamentales como la conectividad y la simple conectividad en espacios tridimensionales.
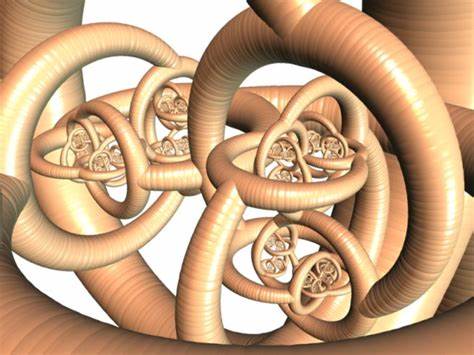
El punto de partida para entender la esfera cornuda es considerar la esfera estándar, una superficie bidimensional en el espacio tridimensional con propiedades muy conocidas y familiares: el interior de esta esfera es simplemente conectado, lo que significa que cualquier lazo o curva dentro del volumen puede ser retraído hasta un punto sin salir del interior. Asimismo, el exterior de la esfera, el espacio fuera de ella, comparte esta propiedad. Sin embargo, la construcción de Alexander trae una ruptura fundamental de esta intuición. El método de construcción de la esfera cornuda comienza con un toro estándar, que puede imaginarse como una dona o un anillo grueso. Se realiza un corte radial por el toro, y en cada lado de ese corte se conecta un pequeño toro, cuyo diseño a su vez se enlaza con el toro en el lado opuesto.
Este proceso no es un simple añadido más sino que se repite infinitamente, generando una estructura crecida en forma de “cuernos” que se interpenetran y entrelazan de manera muy compleja. A medida que esta construcción avanza de forma idealizada hacia el infinito, se obtiene un conjunto límite, una superficie que, a pesar de estar construida a partir de la concatenación infinita de toros, mantiene la propiedad de ser una esfera topológica. Este embebido inusual recibe el nombre de esfera cornuda de Alexander. Resulta particularmente fascinante que, a pesar de la complejidad y la naturaleza “salvaje” de su superficie, la parte interior de esta construcción, conocida como la bola cornuda de Alexander, es simplemente conectada. Esto indica que cualquier curva dentro de esta bola puede ser contraída hasta un punto sin cruzar la superficie.
No obstante, al considerar el espacio fuera de la esfera cornuda, la historia cambia radicalmente: el exterior no es simplemente conectado. Existen lazos que rodean los distintos cuernos y que no pueden ser contraídos a un punto sin atravesar la superficie de la esfera. Este hecho muestra una ruptura directa con el teorema de Jordan-Schönflies, que en dimensiones dos establece que cualquier curva cerrada divide el plano en dos regiones simplemente conectadas, una interior y otra exterior. Sin embargo, Alexander demostró que esta generalización no se extiende al espacio tridimensional para embeddings arbitrarios de esferas, poniendo de manifiesto la complejidad inesperada que surge en dimensiones superiores. Este descubrimiento no solo desafió las nociones tradicionales sino que también marcó la necesidad de distinguir entre diferentes categorías dentro de las variedades topológicas: variedades topológicas, diferenciables y por partes lineales.
Alexander probó que cuando los embeddings son lisos o por piezas lineales, el teorema de Jordan-Schönflies sí se mantiene en tres dimensiones. Por tanto, la esfera cornuda es un ejemplo clásico que motivó a los matemáticos a considerar con mayor rigor esas distinciones, y a estudiar las propiedades de variedades en función de cómo están embebidas. Más allá de su definición y construcción, la esfera cornuda de Alexander tiene propiedades topológicas fascinantes al considerarla dentro de contextos más amplios, como la compactificación uno-puntual del espacio euclidiano tridimensional, conocida como la 3-esfera. Dentro de esta configuración, el espacio que la esfera deja fuera al ser embebida permite la definición de una bola sólida cornuda. Este espacio sólido no es una variedad en sí misma, debido a sus irregularidades y singularidades, pero ha sido objeto de estudio profundo.
El matemático R. H. Bing demostró que si se toma el doble de esta bola sólida—es decir, si se pegan dos copias de la bola cornuda en sus límites correspondientes—el resultado es homeomorfo a la 3-esfera clásica, la esfera tridimensional estándar. Este resultado sorprendente añade una dimensión extra de profundidad al entendimiento de las lesiones o irregularidades en la topología tridimensional y su relación con estructuras clásicas. Las generalizaciones de la construcción de Alexander han abierto nuevas vías para explorar “esferas salvajes” y objetos relacionados en dimensiones superiores y con diferentes configuraciones.
Es posible, por ejemplo, aumentar el número de “cuernos” en cada nivel del proceso iterativo para generar variantes más complejas de la esfera cornuda. Además, existen construcciones distintas pero similares en espíritu, como la esfera cornuda de Antoine, que utiliza el concepto de la cadena de Antoine—otra construcción relacionada con el conjunto de Cantor incrustado de manera patológica—para producir una superficie con propiedades singulares en el espacio tridimensional. Desde una perspectiva histórica y matemática, el estudio de la esfera cornuda ha impulsado la apreciación por los ejemplos patológicos o “salvajes” en topología. Estos ejemplos ponen en tela de juicio la validez de ciertos teoremas y propician la formulación de hipótesis más precisas y refinadas. Además, juegan un papel crucial en la enseñanza y comprensión de la topología, ilustrando claramente que las propiedades intuitivas que funcionan en dimensiones bajas o en ciertas categorías geométricas no son universalmente aplicables.
El impacto de la esfera cornuda de Alexander trasciende la pura topología y llega a campos como la geometría fractal. La superficie resultante no es lisa ni diferenciable en el sentido clásico, exhibiendo una complejidad similar a otras estructuras fractales, lo que permite a los matemáticos pensar en su dimensión y auto-similitud desde una perspectiva contemporánea. Aunque no es un fractal en el sentido estricto, la construcción iterativa infinita que genera sus “cuernos” implica características relacionadas con la auto-similitud y la estructura intrincada a distintas escalas. En términos más amplios, la existencia de objetos como la esfera cornuda de Alexander es un recordatorio de que el espacio tridimensional puede esconder fenómenos inesperados. Desde sus orígenes, las matemáticas han buscado clasificaciones y estructuras ordenadas del espacio, pero ejemplos como este demuestran que la variedad de comportamientos es más rica y compleja.
De hecho, la esfera cornuda invita a reflexionar sobre la naturaleza del espacio y la forma, y sobre cómo las intuiciones basadas en la experiencia visual pueden fallar al abordar problemas topológicos profundos. En la actualidad, la esfera cornuda sigue siendo objeto de estudio y admiración entre matemáticos, no solo por su valor histórico sino también por su papel en investigaciones avanzadas. Su rica topología y las ideas que suscita alimentan nuevas investigaciones en topología tridimensional, teoría de nudos salvajes, y en la comprensión de variedades con singularidades extrañas. Además, sus sofisticados hábitos de enlace y construcción informan modelos en física matemática y en la comprensión del espacio en diversas áreas. Para quienes desean adentrarse en el mundo de la topología algebraica y geométrica, la esfera cornuda ofrece un ejemplo magnífico para comprender la importancia del rigor en definiciones y demostraciones, así como los límites de los teoremas clásicos.
Su estudio también inspira a explorar categorías más allá de la intuición cotidiana, abriendo la puerta a campos más abstractos donde la creatividad matemática y la lógica formal convergen para revelar nuevas dimensiones del conocimiento. En conclusión, la esfera cornuda de Alexander es mucho más que una curiosidad matemática; es un monumento al ingenio humano y a la riqueza oculta en el tejido del espacio. Su descubrimiento marcó un antes y un después en la topología, desafiando conceptos establecidos y forzando a los matemáticos a reconsiderar la naturaleza de la superficie, la conexión y el espacio. Hoy, este objeto sigue iluminando caminos en la matemática pura y aplicada, recordándonos que las estructuras más inesperadas pueden ser las que revolucionen nuestra comprensión del universo.