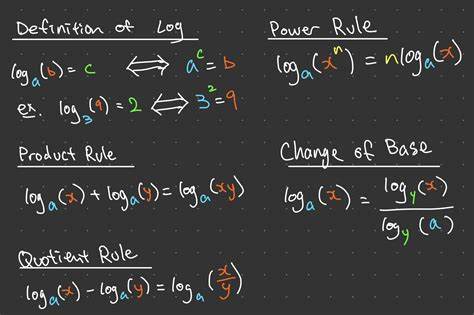En el mundo de la programación y el desarrollo de software, uno de los desafíos comunes es la manipulación y conversión eficiente de números a su representación en cadena de texto, especialmente cuando se trabaja con notaciones científicas o números de gran magnitud. Dentro de este núcleo de tareas, calcular la cantidad de dígitos decimales que posee un número se presenta como una operación fundamental. Aunque puede parecer trivial, el enfoque que se emplee para esta tarea puede impactar significativamente en el rendimiento y la precisión de la aplicación. Para comprender profundamente este problema, es esencial investigar cómo trabajan los exponentes, las cadenas y el logaritmo en base 10, mejor conocido como Log10. Desde las primeras etapas de la formación académica en ciencias de la computación, se enseña que la manera básica de conocer la cantidad de cifras de un entero es dividir ese número repetidamente entre 10 hasta llegar a cero.
Sin embargo, esta técnica iterativa es lenta y poco eficiente cuando se manejan grandes cantidades de datos o números de gran tamaño dentro de sistemas críticos. Por ello, nacen métodos más refinados que se basan en propiedades matemáticas, como el cálculo del logaritmo en base 10, que nos ofrece el exponente de diez necesario para expresar ese número en notación científica, lo cual es directamente equivalente al conteo de dígitos menos uno. El logaritmo base 10 posee una representación matemática sencilla y es muy utilizado para definir la cantidad de dígitos de un número: si log10(n) = x, entonces n tiene aproximadamente x + 1 dígitos. Así, el valor entero de este logaritmo nos indica el orden de magnitud del número, y por lo tanto cuántos dígitos tiene. A pesar de su popularidad teórica, en la práctica el uso directo del log10 presenta varios retos, sobre todo debido a la precisión de los cálculos flotantes y al alto costo que implican las operaciones trascendentales para procesadores tradicionales.
Para poner en contexto, las arquitecturas de procesadores más comunes, como x86 y ARM, no contienen instrucciones de hardware específicas para calcular logaritmos en base 10. En cambio, suelen implementar funciones para logaritmos en base 2 o neperianos, y la transformación hacia log10 se realiza mediante cálculos adicionales que aumentan la latencia y el consumo energético. Esto se debe a que las funciones trascendentales demandan procesamientos complejos, frecuentemente realizados mediante aproximaciones o series, y por ello suelen ser significativamente más lentas que operaciones aritméticas básicas o manipulación directa de bits. Esta limitación impulsa a programadores a buscar alternativas para calcular, por ejemplo, el conteo de dígitos en enteros e incluso en números flotantes, sin la necesidad de recurrir a logaritmos costosos. Un enfoque simplificado consiste en usar comparaciones directas con potencias predefinidas de 10 para determinar el rango en el que se encuentra el número.
Por ejemplo, para un entero de 8 bits, basta con verificar si es mayor o igual que 100 o 10 para saber si tiene 3, 2 o 1 dígito respectivamente. Este método es sorprendentemente eficiente para rangos pequeños, pues evita la ejecución de funciones matemáticas y reduce la lógica a simples comparaciones que suelen ser optimizadas por el compilador e incluso predecidas correctamente por el procesador. Sin embargo, esta técnica también tiene sus inconvenientes. Al involucrar varias sentencias condicionales, se incrementa la probabilidad de incurriendo en predicciones erróneas de rama (branch mispredictions) dentro del pipeline del CPU, que son operaciones costosas y frenan el rendimiento. Para mitigar esto, algunos desarrolladores aplican estrategias que evalúan todas las condiciones y combinan sus resultados, eliminando ramas condicionales e incrementando la paralelización de instrucciones a nivel de CPU, aunque esto puede derivar en mayor carga computacional debido al volumen de operaciones realizadas.
Cuando el enfoque se traslada a enteros de 32 o 64 bits, la complejidad y el rango de valores aumentan considerablemente. Utilizar comparaciones lineales se vuelve poco práctico, por lo que aparece la alternativa siempre rápida y sencilla de calcular logaritmos en base 2 – una operación muy bien optimizada en la mayoría de hardware actuales a través de instrucciones específicas como LZCNT – y luego usar una tabla de búsqueda precalculada que asocia valores de log2 a cantidades de dígitos decimales. Este método, empleado incluso en extensas librerías estándar de lenguajes como C# en .NET, ofrece un equilibrio eficiente entre precisión y velocidad sin necesidad de operaciones aritméticas pesadas. Una implementación popular consta en obtener el logaritmo base 2 del entero evaluado, indexar una tabla con constantes mágicas cuidadosamente calculadas para cada posible resultado, y sumar el desplazamiento adecuado para retornar el conteo preciso de dígitos.
Este mecanismo hace que la operación sea casi instantánea, limitándose básicamente al cómputo del log2 y a una pequeña búsqueda en memoria, lo que es mucho más eficiente que el cálculo matemático directo del log10. Ahora bien, al considerar números en punto flotante, el panorama cambia y se vuelve más complejo. Los números en coma flotante representan valores en base 2, con mantisa y exponente binario, lo que complica directamente la obtención del logaritmo decimal. Para casos que requieran manipular números con exponentes extremadamente grandes, como en ciertos modelos científicos o financieros, se tiende a utilizar tipos de dato personalizados que almacenan la mantisa en un float o double (de 32 o 64 bits) y el exponente en un entero de 64 bits, representando el valor como mantisa multiplicada por 10 elevado a la potencia del exponente. En este contexto, resulta crucial normalizar números después de operaciones matemáticas para mantener la mantisa en un rango estándar, como [1, 10), lo que implica conocer el logaritmo base 10 del valor parcial.
Dado que las funciones de logaritmos estándar son lentas y consume recursos, se puede apostar por soluciones híbridas con comparaciones directas entre rangos predefinidos usando potencias de diez y una única llamada a la función logarítmica cuando el número rebasa ciertos umbrales. Esta aproximación minimiza el uso de operaciones costosas al tiempo que provee rapidez en la mayoría de casos. Más allá de las soluciones técnicas, un aspecto relevante es cómo los entornos de ejecución modernos, tales como el Runtime de .NET, optimizan sus funciones nativas como ToString para enteros y flotantes. Por ejemplo, .
NET emplea caché de cadenas para números pequeños que evita la creación repetitiva de objetos en memoria, acelerando dramáticamente la conversión y lectura de dígitos. Esto demuestra que a veces, la elección del algoritmo debe conjugarse con la plataforma y sus optimizaciones internas para obtener el mejor rendimiento real en producción. Adicionalmente, el impacto real de ramificación en el microprocesador no debe subestimarse. Cuando las instrucciones condicionales se ejecutan en secuencia con valores altamente variados que confunden el predictor de ramas, el desempeño puede degradarse notablemente. Por ello, los desarrolladores deben plantear escenarios que prueben las funcionalidades con patrones de datos variados para medir el impacto de las predicciones erróneas y ajustar sus algoritmos para minimizar latencias inesperadas.
La posibilidad de implementar soluciones basadas en análisis bit a bit y operaciones a nivel bajo, usando instrucciones como conteo de ceros a la izquierda (leading zero count) ha sido explotada extensamente en librerías estándar y ha resultado ser una vía efectiva para mejorar el conteo de dígitos en enteros. La ausencia de instrucciones de hardware para logaritmos en base 10 fuerza a confiar en estas técnicas que combinan matemáticas discretas y optimización de hardware para salvaguardar la velocidad sin sacrificar precisión. En conclusión, el análisis y manejo de cadenas, exponentes y logaritmos base 10 tiene un papel crítico en la forma en que los sistemas computacionales procesan y representan números. Optar por el método adecuado depende no solo del tamaño y tipo de datos, sino también de la plataforma de ejecución y la naturaleza del problema. La combinación de soluciones geométricas como logaritmos base 2 acompañadas de tablas precomputadas, el uso prudente de comparaciones de rango para acelerar los casos comunes, y la consideración del impacto en la arquitectura del procesador, resultan en mejoras sustanciales para cualquier desarrollador que busque un cómputo eficiente y efectivo.
En tiempos donde el rendimiento y la precisión son claves, dominar estas técnicas se convierte en una ventaja competitiva indispensable.