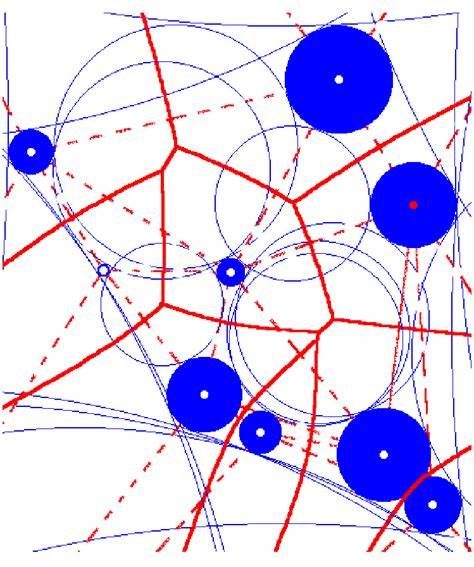
Los diagramas de Voronoi son una herramienta fundamental en geometría computacional y tienen innumerables aplicaciones que abarcan desde la ciencia de datos hasta la biología y la ingeniería. Específicamente, los diagramas de Voronoi ponderados han capturado la atención de investigadores por su capacidad para modelar relaciones espaciales con influencias relativas o pesos asociados a los puntos generadores. Dentro de esta categoría, el diagrama de Voronoi sumamente ponderado o aditivo es especialmente fascinante debido a la manera en que modifica la distancia tradicional para generar regiones de influencia que reflejan condiciones reales más complejas. Un diagrama de Voronoi típico divide un espacio en regiones donde cada punto dentro de una región está más cerca de un sitio especificado que de cualquier otro. Sin embargo, en muchas situaciones prácticas, no todos los puntos generadores tienen la misma influencia.
Esto puede ser debido a factores como tamaño, capacidad o importancia. Para modelar esto, el diagrama de Voronoi ponderado introduce pesos a cada punto generador. En el caso del diagrama de Voronoi sumamente ponderado, a cada distancia euclidiana hacia un punto se le resta un peso positivo, lo que tiene como resultado regiones que no sólo dependen de la proximidad sino también de la magnitud del peso asociado. Matemáticamente, si consideramos un conjunto de puntos en el plano, cada punto tiene un peso asignado. La distancia ponderada de un punto cualquiera en el plano a un sitio generador es la distancia euclidiana al sitio menos su peso.
La región de Voronoi correspondiente a ese sitio se define entonces como el conjunto de puntos cuya distancia ponderada a ese sitio es menor que a cualquier otro sitio con peso. Esta simple modificación resulta en diagramas con estructuras notablemente distintas a los diagramas de Voronoi tradicionales. Una de las características más interesantes de este diagrama es que sus bordes entre regiones no son lineales en general, sino que pueden tomar la forma de arcos hiperbólicos o segmentos rectos dependiendo de la configuración de los pesos y la posición de los puntos generadores. Por esta razón, el diagrama también es conocido como teselación de Dirichlet hiperbólica. Esta expresión subraya la riqueza geométrica y analítica que subyace en su construcción y el papel relevante que juega la geometría hiperbólica en la descripción de sus bordes.
Las aplicaciones prácticas de los diagramas de Voronoi ponderados son muy diversas. En geografía y planificación urbana, estos diagramas permiten modelar zonas de influencia que consideran no sólo la distancia sino también factores como la capacidad o popularidad de un punto de servicio, como un hospital o una estación de transporte público. Esto es esencial para un análisis de accesibilidad más realista y para la correcta asignación de recursos. En biología, los diagramas ponderados se utilizan para modelar sistemas donde distintos objetos o entidades tienen pesos o tamaños variados que afectan su dominio de influencia, como en la distribución de células o en el estudio de regiones de crecimiento de tejidos. Esto permite nuevas perspectivas para entender cómo las propiedades físicas y biológicas interactúan para formar patrones espaciales complejos.
Dentro del campo de la informática gráfica y visión por computadora, la capacidad de modelar regiones de influencia ponderadas facilita la segmentación de imágenes y la generación de mallas adaptativas para simulaciones numéricas. Al considerar pesos, se pueden manejar con mayor precisión zonas donde ciertos objetos tienen un impacto predominante, lo que mejora la calidad y la eficiencia en el procesamiento. Desde el punto de vista teórico, el estudio de los diagramas de Voronoi sumamente ponderados implica desafíos matemáticos particulares. La presencia de pesos que se restan a la distancia genera no convexidad en las regiones, dificultades en la computación precisa y en la representación gráfica. Existen algoritmos especializados que permiten su construcción, algunos aprovechando transformaciones geométricas y propiedades de la geometría hiperbólica para simplificar la obtención de bordes y vértices.
Diversos softwares y librerías de visualización y cálculo geométrico han incorporado funcionalidades para trabajar con diagramas de Voronoi ponderados. Disponibilidad de código fuente y herramientas abiertas permite a investigadores y profesionales explorar estas estructuras para aplicaciones personalizadas, potenciar estudios académicos o resolver problemas complejos de división espacial. Un aspecto crítico para optimizar el uso de los diagramas de Voronoi ponderados es la selección adecuada de los pesos. La relación entre los pesos y las posiciones de los puntos debe considerarse cuidadosamente para evitar resultados inadecuados, como regiones degeneradas o la ausencia de zonas de influencia. La calibración puede portar información relevante sobre la dinámica que se esté modelando, haciendo que la interpretación de los resultados sea tan valiosa como la generación misma del diagrama.
En resumen, los diagramas de Voronoi sumamente ponderados ofrecen un marco robusto y versátil para modelar espacios con influencia desigual, ampliando las posibilidades que ofrecen los diagramas clásicos. Su estudio involucra una combinación fascinante de geometría euclidiana y no euclidiana, algoritmos computacionales avanzados y aplicaciones prácticas en áreas tan variadas como la geografía, biología, informática y planificación urbana. Continuar investigando y desarrollando estas estructuras abre el camino para nuevas soluciones eficientes a problemas complejos, al tiempo que profundiza la comprensión matemática de las interacciones espaciales. En un mundo donde la precisión y la adaptabilidad en la modelización espacial son cada vez más esenciales, los diagramas de Voronoi ponderados permanecen como una herramienta clave para los expertos en ciencia y tecnología.