En los últimos años, el estudio de estructuras ópticas cada vez más complejas ha capturado la atención de científicos y tecnólogos alrededor del mundo. Entre ellas, los nudos ópticos, que son configuraciones en el campo electromagnético donde las líneas de singularidad de fase forman enlaces y nudos en tres dimensiones, representan un fascinante y prometedor campo de investigación. La naturaleza topológica de estos nudos sugiere una resistencia inherente a perturbaciones, lo que plantea el escenario ideal para aplicaciones en comunicaciones, microfabricación y computación avanzada. Sin embargo, el comportamiento real de estos nudos ópticos cuando atraviesan medios perturbativos como la atmósfera terrestre, donde la turbulencia juega un papel fundamental, era hasta hace poco un misterio. La comprensión de la estabilidad de estos nudos ópticos en condiciones de turbulencia atmosférica abre una puerta para aprovechar sus propiedades en entornos reales y desafiantes, que van desde las comunicaciones hasta la metrología y la imagenología biomédica.
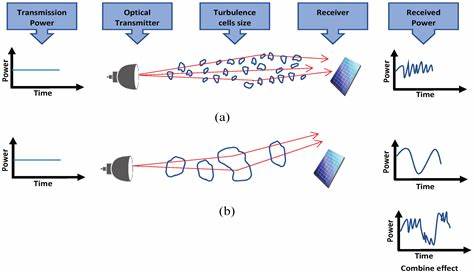
La turbulencia atmosférica es un fenómeno universal que se manifiesta en muchos contextos naturales y tecnológicos, desde la cúpula terrestre hasta escenarios astronómicos. Esta turbulencia genera variaciones rápidas e impredecibles en el índice de refracción del aire debido a fluctuaciones térmicas y convectivas. Como consecuencia, las ondas ópticas que viajan a través de este medio experimentan distorsiones significativas en su frente de fase y su intensidad, fenómeno conocido como distorsión de la fase, scintilación y deriva del haz. Estos efectos desafían la integridad de cualquier señal óptica, especialmente aquellas con estructuras topológicas complejas, como los nudos ópticos. Los nudos ópticos pueden concebirse formalmente como el anidamiento de un círculo dentro del espacio euclidiano tridimensional, donde las líneas de singularidades de fase de un haz luminoso forman configuraciones cerradas y entrelazadas.
Inicialmente predichos en el campo no paraxial mediante la superposición de haces Bessel, estos nudos fueron posteriormente representados experimentalmente por combinación de modos Laguerre-Gaussian (LG), que permiten controlar tanto la fase como la polarización. Un ejemplo icónico es el nudo trifoliado, una configuración en la que las líneas de singularidad forman un lazo con tres cruces, que dependiendo de su forma, puede resistir diversas perturbaciones sin perder la conectividad principal, es decir, su topología. La topología, como rama de las matemáticas, ofrece predicciones poderosas sobre la robustez de los nudos. Según el concepto de isotopía ambiental, dos nudos son topológicamente equivalentes si uno puede deformarse en el otro sin cortes ni auto-intersecciones. Aun así, este ideal matemático no garantiza que las estructuras físicas mantengan sus propiedades en medios reales con perturbaciones, como la atmósfera turbulenta.
Esta es la frontera crítica que ha motivado un reciente estudio experimental y teórico que evalúa la estabilidad real de los nudos ópticos bajo condiciones de turbulencia controlada. Para recrear fielmente las condiciones atmosféricas en laboratorio, se emplearon cámaras turbulentas con flujo de aire caliente, junto con dispositivos moduladores espaciales de luz (SLM) para codificar las formas nódicas en haces ópticos a una longitud de onda verde estándar de 532 nanómetros. Esta configuración permitió, mediante interferometría, medir modulación de fase y amplitud del campo eléctrico, produciendo reconstrucciones tridimensionales precisas de las líneas de singularidad, con un seguimiento exacto de su posible deformación o ruptura. Complementariamente, las simulaciones numéricas implementaron múltiples pantallas de fase que reproducen el espectro de potencia de Kolmogorov característico de la turbulencia atmosférica, ajustando parámetros clave como la varianza Rytov y el parámetro de estructura del índice de refracción, para evaluar su influencia en la dinámica de los nudos. Los resultados revelaron que en regímenes de turbulencia débil, los nudos ópticos mantienen su integridad topológica con una alta probabilidad, confirmando la hipótesis inicial de robustez basada en la topología matemática.
Sin embargo, cuando la turbulencia se intensifica, se observaron eventos de reconexión de las líneas de singularidad, en los que las configuraciones nódicas se transforman en otras estructuras topológicas, como enlaces Hopf o incluso nudos trivialmente sin enredos. Estas transiciones topológicas ocurren debido a la inducción de modos ópticos adicionales que interactúan y redistribuyen las líneas de fase, fenómeno análogo a la ruptura de vortex en superfluidos descrita por la ecuación de Gross-Pitaevskii. Para mitigar estos efectos negativos, el estudio desarrolló un algoritmo de optimización que ajusta los coeficientes de amplitud de los modos Laguerre-Gaussian constituyentes, maximizando la distancia entre singularidades en cada plano longitudinal. Esta estrategia, llamada optimización de posición singular, no solo facilita la medición precisa de los nudos ópticos en presencia de turbulencia, sino que también mejora su estabilidad al reducir la probabilidad de reconexiones y pérdidas topológicas. Los experimentos confirmaron que esta optimización supera en rendimiento a métodos previos basados únicamente en la distribución intensitaria, marcando un avance significativo para futuras aplicaciones.
Además, la investigación demostró un comportamiento interesante respecto al contraste de amplitud alrededor de los puntos singulares: los nodos con mayor contraste presentan menor deriva ante la turbulencia. Esto implica que diseñar nudos ópticos con un perfil de amplitud más potente localmente puede protegerlos aún más de las turbulencias naturales. Sin embargo, el estudio también señaló que en medias turbulentas severas, la conservación estricta de la topología clásica (basada en el número de cruces) puede no ser la forma más precisa de clasificar las estructuras recuperadas, dado que patrones tridimensionales deformados pueden mantener propiedades intrínsecas del nudo original, aunque el conteo formal cambie. Esto sugiere la necesidad de nuevos invariantes o criterios, centrados en propiedades espaciales tridimensionales, para clasificar y aprovechar eficazmente los nudos en condiciones adversas. Los hallazgos no solo ofrecen una mejor comprensión fundamental de la interacción entre luz estructurada y medios complejos, sino que también abren la puerta a una nueva generación de tecnologías ópticas robustas.
En comunicaciones clásicas y cuánticas, la utilización de nudos y enlaces permite codificar información en el dominio espacial y topológico del campo lumínico, ofreciendo resistencia ante interferencias y pérdidas. La microfabricación con luz estructurada, fundamental para crear dispositivos tridimensionales a escala microscópica, podría aprovechar esta estabilidad para lograr estructuras complejas más precisas y resistentes. Asimismo, las implicaciones para la computación cuántica basadas en estados topológicos no pueden subestimarse. Los nudos ópticos podrían actuar como portadores de información topológica, difíciles de corromper y con potencial para operaciones lógicas más estables. Además, en campos emergentes como la imagenología biomédica y el control de la materia a través de la luz, comprender y aprovechar la estabilidad de estructuras topológicas frente a perturbaciones es crucial para desarrollar técnicas más eficientes y resistentes.
En conclusión, el estudio reciente sobre la estabilidad de nudos ópticos en turbulencia atmosférica representa un hito en la física aplicada y la óptica. Aunque la topología matemática predice estabilidad ideal, la realidad de los medios turbulentos demuestra un panorama más complejo, donde pérdidas y transformaciones topológicas pueden ocurrir, particularmente en condiciones severas. Sin embargo, con estrategias de optimización y nuevas perspectivas en clasificación, es posible preservar y controlar estas estructuras sofisticadas, potenciando su aplicabilidad en múltiples disciplinas. La senda hacia un futuro dominado por la óptica topológica está definitivamente abierta, con desafíos apasionantes que delinean el horizonte científico y tecnológico.