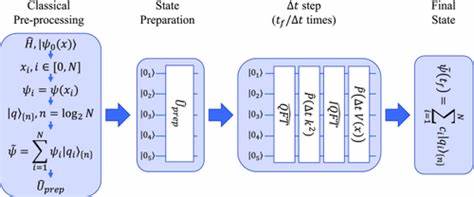
El cómputo cuántico es una revolucionaria disciplina que aprovecha las propiedades fundamentales de la mecánica cuántica para resolver problemas que son intratables para las computadoras clásicas. En las últimas décadas, el desarrollo de algoritmos cuánticos ha despertado un gran interés en la comunidad científica y tecnológica, y con la llegada de plataformas accesibles como IBM Q, los principiantes tienen ahora la oportunidad de experimentar con estos algoritmos en hardware real. Esta guía está diseñada para introducir a los lectores en el fascinante mundo de las implementaciones de algoritmos cuánticos, desde sus fundamentos hasta ejemplos prácticos que pueden ser ejecutados en computadoras cuánticas de pocos qubits. Para comenzar, es esencial comprender el concepto del qubit, la unidad básica de información cuántica. A diferencia del bit clásico que solo puede estar en estado 0 o 1, el qubit puede existir en una superposición de ambos estados, lo que se representa como |φ⟩ = α|0⟩ + β|1⟩, donde α y β son amplitudes complejas que cumplen con la condición de normalización |α|^2 + |β|^2 = 1.
Esta capacidad de superposición es la base del poder computacional cuántico. Además, cuando hablamos de sistemas de múltiples qubits, el espacio de estados crece exponencialmente, y pueden formarse estados entrelazados que no se pueden descomponer en productos de estados individuales — el entrelazamiento es otra propiedad esencial que potencia los algoritmos cuánticos. El desarrollo del modelo de programación cuántica ha sido un hito clave para que los científicos e ingenieros puedan expresar algoritmos cuánticos sin profundizar demasiado en los fundamentos físicos. En este modelo, las operaciones sobre qubits se implementan mediante puertas cuánticas, que son transformaciones unitarias reversibles análogas a las puertas lógicas clásicas, pero respetando las restricciones propias del mundo cuántico. Algunas de las puertas cuánticas más comunes incluyen la Hadamard, que genera superposiciones, las puertas Pauli X, Y, Z que corresponden a rotaciones sobre el espacio de estados, y puertas de control como la CNOT, que permiten crear entrelazamiento entre qubits.
El uso de diagramas de circuitos cuánticos facilita la visualización e implementación de algoritmos, donde cada línea representa un qubit y los bloques indican la aplicación sucesiva de puertas. Por ejemplo, la preparación del estado Bell, un estado de dos qubits entrelazados, se logra aplicando una puerta Hadamard en el primer qubit seguida de una puerta CNOT que usa este qubit como control y el segundo como objetivo. Medir ambos qubits en este estado entrega resultados correlacionados que evidencian el fenómeno de entrelazamiento. En cuanto a la ejecución práctica, la plataforma IBM Q es pionera en permitir el acceso público a computadoras cuánticas reales a través de la nube. Modelos como el ibmqx4, de cinco qubits, son ideales para principiantes debido a su disponibilidad y documentación detallada.
Sin embargo, hay que tener en cuenta ciertas limitaciones actuales como la conectividad restringida entre qubits, lo cual significa que solo ciertas combinaciones de qubits pueden interactuar directamente mediante puertas controladas, y los efectos del ruido de hardware que afectan la fidelidad de las operaciones y la decoherencia, limitando la profundidad de los circuitos que se pueden ejecutar con éxito. Para facilitar la creación y ejecución de algoritmos cuánticos en dicha plataforma, IBM provee el SDK Qiskit. Esta biblioteca open source permite programar circuitos en un entorno familiar para programadores clásicos, en Python, facilitando desde la definición del circuito cuántico, pasando por la simulación en computadoras clásicas, hasta la ejecución en hardware real. La biblioteca ofrece elementos para crear circuitos dinámicos, configurar diferentes backends, y analizar resultados. Una de las contribuciones más relevantes para que los principiantes se acerquen a la programación cuántica ha sido la implementación práctica de algoritmos fundamentales, tales como el algoritmo de Grover.
Este algoritmo ofrece una ventaja cuadrática en la búsqueda dentro de bases de datos no estructuradas, lograda mediante la aplicación repetida de un operador difusor sobre superposiciones iniciales, amplificando la amplitud del estado deseado. En su implementación, se requiere la construcción de un oráculo cuántico reversible que marque el estado objetivo, comúnmente representado en hardware actual como una compuerta Toffoli adaptada a los qubits disponibles. El desarrollo de circuitos optimizados para un número restringido de qubits y la adaptación a la topología física del dispositivo son factores críticos para mejorar la fidelidad de los resultados. Otro algoritmo emblemático es el de Bernstein-Vazirani, que permite identificar una cadena oculta binaria con una única consulta al oráculo, a diferencia del caso clásico que requiere un número de consultas proporcional al tamaño de la cadena. Su implementación demuestra cómo aprovechar la interferencia cuántica y la transformada de Hadamard para obtener información global de una función, siguiendo un procedimiento que por el momento se adapta bien a las limitaciones de los modelos actuales de computación cuántica.
En problemas más complejos, como la resolución de sistemas lineales mediante el algoritmo HHL, se exhibe el enorme potencial teórico del cómputo cuántico para acelerar problemas clásicos. Este algoritmo, aunque desafiante para implementar completamente en hardware actual debido a la profundidad y cantidad de qubits requeridos, ha sido adaptado para casos pequeños y ha mostrado buenas aproximaciones en simuladores y pequeñas máquinas reales. El uso de técnicas auxiliares como la estimación de fases y la transformada cuántica de Fourier permiten la diagonalización eficiente de matrices, siendo herramientas recurrentes en la mayoría de los algoritmos cuánticos. Una de las implementaciones más sorprendentes de la computación cuántica es la factorización entera con el algoritmo de Shor, cuyos fundamentos continúan renovando el interés, dada su potencial para romper esquemas criptográficos clásicos. Mediante la reducción del problema de factorización al de encontrar el período de una función y el uso de la transformada cuántica de Fourier, este algoritmo ha sido reproducido en experimentos con números pequeños en hardware real, mostrando los primeros pasos hacia futuras aplicaciones prácticas.
Paralelamente, los métodos de algoritmia cuántica también apuestan por nuevas estructuras matemáticas, como el análisis de representaciones de grupos, una área donde el algoritmo conocido como Hadamard test facilita el cálculo de elementos matriciales esenciales en la teoría de grupos. Estas aplicaciones, además de potenciar problemas teóricos, abren caminos hacia algoritmos especializados en física, química cuántica, y optimización matemática. Al mismo tiempo, el cómputo cuántico aplicado a grafos encuentra en las caminatas cuánticas y el algoritmo aproximado cuántico para optimización (QAOA) ecos ideales para demostrar un poder de cálculo superior o complementario al clásico. En particular, establecer el estado equilibrio o mínimo de energía en modelos como el Ising transversal o identificar árboles de recubrimiento mínimos se transforman en retos alcanzables para computadoras con pocos qubits y mediante circuitos cuánticos especialmente diseñados. Dado el comportamiento probabilístico intrínseco del cómputo cuántico, surgen métodos para maximizar la probabilidad de éxito, tales como la amplificación de amplitud, una generalización elegante de Grover, que reduce el número de repeticiones necesarias para obtener resultados confiables.
Esta técnica es crucial en la verificación de productos matriciales y en la mejora de búsqueda de soluciones óptimas en listas y espacios enormes. No obstante, es fundamental destacar que el verdadero crecimiento del cómputo cuántico dependerá en gran medida del desarrollo de esquemas de corrección de errores que permitan mitigar la decoherencia y la fidelidad imperfecta de las puertas cuánticas. Experimentos actuales muestran que, en algunas circunstancias básicas, la codificación para proteger un qubit contra errores puede no ofrecer una mejora significativa en la precisión global, debido al sobrecosto de aplicar gates adicionales que también pueden introducir ruido. Este es un campo vibrante de investigación que condicionará la escalabilidad práctica de las tecnologías cuánticas en los años venideros. Para quienes buscan iniciarse en esta disciplina, es recomendable explorar entornos de simulación robustos y progresar en la comprensión de las propiedades matemáticas subyacentes, como la representación vectorial de estados, las transformaciones unitarias y los conceptos básicos de álgebra linear aplicados al espacio de Hilbert.
La comunidad cuántica también cuenta con repositorios abiertos de código y ejemplos que cubren desde los algoritmos más sencillos hasta protocolos complejos. Finalmente, el camino hacia la computación cuántica universal es un viaje apasionante lleno de desafíos técnicos y conceptuales, pero la evolución constante del hardware, junto con la creación de nuevos algoritmos y técnicas de programación, abren amplias posibilidades tanto para investigadores como para desarrolladores. El dominio de las implementaciones básicas no solo permite familiarizarse con esta tecnología disruptiva, sino que también sienta las bases para contribuir en el diseño de futuras aplicaciones que transformarán ámbitos tan variados como la criptografía, la química computacional, la inteligencia artificial y la simulación de sistemas físicos complejos.