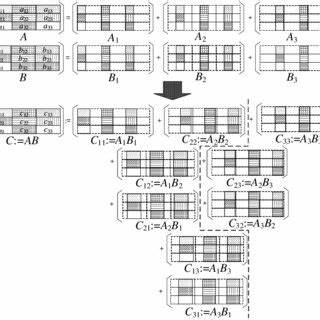
La multiplicación de matrices es una operación fundamental en computación científica, gráficos por computadora, inteligencia artificial y muchos otros campos tecnológicos. Especialmente cuando se trata de aritmética de punto flotante (FP), la eficiencia y precisión de esta operación pueden determinar el rendimiento general de sistemas complejos como simuladores, modelos de aprendizaje profundo y aplicaciones matemáticas avanzadas. En este contexto, el Ozaki Scheme II emerge como una innovación significativa al combinar principios matemáticos clásicos con las capacidades modernas del hardware para lograr una emulación eficiente de la multiplicación de matrices en punto flotante utilizando operaciones enteras. La importancia de las rutinas GEMM (General Matrix-Matrix Multiplication) no se puede subestimar, ya que representan el núcleo de la librería BLAS (Basic Linear Algebra Subprograms), ampliamente empleada para ejecutar multiplicaciones matriciales optimizadas. Sin embargo, a pesar de la optimización derivada de arquitecturas específicas, las operaciones con punto flotante de alta precisión suelen ser costosas en términos de recursos computacionales.
Es aquí donde el esquema Ozaki clásico propuso una emulación mediante la descomposición de matrices de entrada en componentes de baja precisión, permitiendo que la suma de las operaciones parciales reproduzca con exactitud el resultado en alta precisión. Ozaki Scheme II amplía esta idea y la adapta para aprovechar la aritmética modular y la famosa Teoría de los Restos Chinos (Chinese Remainder Theorem, CRT). Este enfoque no solo mantiene la eficiencia computacional inherente a los GEMM altamente optimizados, sino que además ofrece un control flexible sobre el número de multiplicaciones matriciales realizadas. Esto se traduce en una mejora en la precisión del cálculo, pudiendo ajustar el nivel de exactitud según el requerimiento de la aplicación. Los experimentos numéricos presentados comprueban el poder práctico de esta técnica, especialmente al utilizar operaciones INT8 en Tensor Cores de GPUs, combinadas con cálculos en FP64 en CPUs.
Por ejemplo, cuando se implementa esta estrategia en la GPU NVIDIA RTX 4090, se alcanzan velocidades de hasta 9.8 TFLOPS, superando la ejecución nativa de FP64. En GPUs más potentes como la NVIDIA GH200, las cifras son aún más impresionantes, llegando hasta 80.2 TFLOPS. Esto indica que la emulación mediante operaciones enteras y modularidad no solamente es viable sino competitiva en términos de rendimiento.
En el espacio de las CPUs, Ozaki Scheme II también demuestra ventajas claras. La emulación de aritmética de precisión cuádruple, tradicionalmente una tarea intensiva, alcanza hasta 2.3 veces más velocidad que los métodos convencionales basados en el esquema Ozaki original. Esta mejora abre nuevas posibilidades para aplicaciones científicas y de ingeniería que dependen de cálculos numéricos extremadamente precisos pero demandantes. El secreto detrás de estas ventajas radica en la aplicación de la Teoría de los Restos Chinos para reconstruir números de alta precisión a partir de múltiples componentes modulares.
A diferencia de la descomposición decimal o en fracciones binarias bajas, la CRT permite dividir los números en segmentos que pueden procesarse con precisión en enteros, cuyos resultados luego se combinan para obtener el producto acumulado con alta fidelidad. Además, el esquema incorpora técnicas para manejar la propagación del error numérico, un aspecto crítico cuando se trabaja con aritmética de punto flotante. Al controlar la cantidad de particiones y ajustar la granularidad del procesamiento modular, Ozaki Scheme II garantiza una reducción significativa de las imprecisiones, que suele ser un desafío mayor en multiplicaciones matriciales de alta dimensión. Este método encuentra una sinergia perfecta con la evolución del hardware, donde los núcleos Tensor y las instrucciones INT8 ofrecen paralelismo masivo y veloces velocidades de operación. El aprovechamiento de estas características permite no solo acelerar cálculos, sino también optimizar el consumo energético y los recursos computacionales, aspectos clave en centros de datos y supercomputadoras.
Para desarrolladores y científicos de datos, Ozaki Scheme II ofrece una nueva vía para implementar algoritmos numéricos robustos en plataformas de hardware heterogéneas. La adaptabilidad del método facilita su integración en sistemas que combinan CPUs tradicionales con GPUs aceleradas, creando un entorno de computación híbrido que maximiza tanto la precisión como la eficiencia. Finalmente, el impacto potencial de esta técnica va más allá de multiplicaciones matriciales. La capacidad de emular operaciones de punto flotante en enteros con alta performance puede estimular avances en áreas como criptografía, simulación física y procesamiento de señales, donde las necesidades de cálculo preciso y rápido son constantes. En resumen, Ozaki Scheme II representa un avance notable en la emulación de multiplicación de matrices en punto flotante, combinando matemáticas clásicas con ingeniería de vanguardia para superar limitaciones técnicas tradicionales.
La conjunción de la teoría modular con la potencia de hardware moderno abre camino a optimizaciones que pueden transformar la forma en que se procesan datos numéricos en la ciencia y la industria actual.