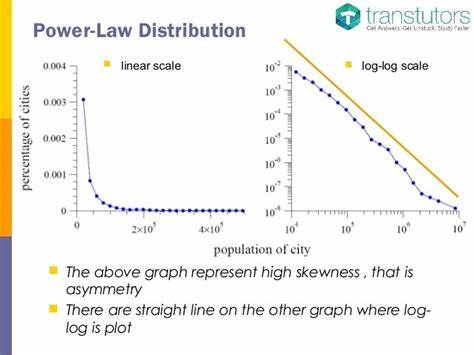
Las leyes, las leyes de potencia y la estadística: desentrañando el enigma del universo En el vasto campo de la ciencia, las leyes que rigen el comportamiento de la naturaleza son esenciales para nuestra comprensión del mundo. Desde la caída de una manzana hasta las complejidades del clima, estas leyes son el marco que nos permite interpretar los fenómenos que nos rodean. Sin embargo, entre estas leyes, las llamadas "leyes de potencia" han capturado la atención de científicos e investigadores en varias disciplinas, desde la geofísica hasta la biología, desafiando nuestras nociones tradicionales sobre las relaciones matemáticas en la naturaleza. ¿Qué son exactamente las leyes de potencia? En términos simples, una ley de potencia es una relación matemática que describe cómo una cantidad responde a otra en términos de su magnitud. En un gráfico de logaritmos, una ley de potencia se representa como una línea recta, lo que sugiere que existe un patrón subyacente que puede ser evidente a través de grandes conjuntos de datos.
Uno de los ejemplos más conocidos de esta ley es la Ley de Gutenberg-Richter, que sugiere que la probabilidad de que ocurra un terremoto de cierta magnitud disminuye en función de la energía liberada. Es decir, los terremotos más grandes son raros, mientras que los más pequeños son más comunes. A pesar de su elegancia, las leyes de potencia han sido objeto de controversia, especialmente en el contexto del análisis de datos. El científico Mark Buchanan, en su artículo para "Nature Physics", destaca que, aunque el análisis de datos puede parecer un ejercicio técnico seco, es esencial para validar teorías científicas. De hecho, Buchanan advierte sobre los peligros de sacar conclusiones precipitadas de los datos, especialmente cuando estos son escasos o de mala calidad.
En el ámbito científico, se dice con frecuencia que "los datos hablan", pero ¿qué sucede cuando esos datos son confusos o contradictorios? La interpretación de datos basados en regresiones lineales ha generado múltiples dudas en la comunidad científica. Durante décadas, muchos investigadores han afirmado que la relación entre diferentes variables sigue una ley de potencia, respaldando sus afirmaciones con análisis estadísticos. Sin embargo, Clauset y sus colegas han demostrado que el uso sin restricciones de técnicas de regresión puede conducir a errores significativos. Este hallazgo subraya la importancia de someter los datos a un análisis riguroso y consciente. Un punto clave que resalta Buchanan es que, si bien las leyes de potencia pueden describir aspectos de varios fenómenos naturales, la validación de estas leyes requiere un enfoque más metódico.
El primer paso es evaluar la probabilidad de que los datos observados podrían surgir de un proceso de ley de potencia. Esto implica un análisis más sofisticado que simplemente graficar datos en un diagrama de logaritmos y reclamar una correlación. En lugar de eso, se sugiere utilizar métodos estadísticos más robustos que evalúen la similitud entre la función de distribución acumulativa de los datos reales y la función de distribución de una hipotética ley de potencia. La estadística, que a menudo se percibe como un componente aburrido de la ciencia, se vuelve crucial en este contexto. A través de métodos estadísticos, los científicos pueden discernir patrones verdaderamente significativos y separar los efectos de la aleatoriedad de las correlaciones genuinas.
La necesidad de un enfoque reflexivo en el análisis de datos no solo es crucial para la validación de leyes de potencia, sino también para la ciencia en general. La tentación de caer en la trampa del "pensamiento deseoso" es alta, y la historia está repleta de ejemplos donde los investigadores se han aferrado a teorías que carecen de fundamento empírico. La re-evaluación de conjuntos de datos que previamente habían sido señalados como que seguían una ley de potencia es fundamental. En su estudio, Clauset y sus colegas examinan 24 conjuntos de datos del mundo real relacionados con este fenómeno, descubriendo que, si bien algunos datos, como los de incendios forestales y la distribución de enlaces en la red, encajan moderadamente en una ley de potencia, otros, como la distribución de la riqueza, no presentan dicha configuración. Este descubrimiento pone de relieve una cuestión crítica: aunque las leyes de potencia pueden tener aplicaciones prácticas y explicar ciertos fenómenos, no son una panacea ni un marco universal que se pueda aplicar a todos los datos.
Esta reflexión sobre los límites y las aplicaciones de las leyes de potencia también resuena en los campos de la biología y la sociología, donde las condiciones complejas e interconectadas presentan un desafío adicional en el análisis de datos. En tales contextos, el uso de modelos de ley de potencia puede simplificar en exceso la rica diversidad de procesos subyacentes, llevando a interpretaciones erróneas sobre la dinámica social o ecológica. Las implicancias de estas revelaciones son significativas. En un tiempo donde la ciencia está cada vez más influenciada por la disponibilidad de grandes volúmenes de datos, la importancia de la calidad del análisis estadístico se vuelve imperativa. Las técnicas modernas de análisis de datos, facilitadas por software estadístico accesible, pueden, si no se usan correctamente, llevar a conclusiones incorrectas que perpetúan conceptos erróneos dentro de la comunidad científica y el público en general.
La tendencia actual a utilizar modelos de ley de potencia es un recordatorio de que la ciencia avanza no solo a través de la acumulación de datos, sino a través de un enfoque crítico y reflexivo hacia los mismos. Las leyes de potencia pueden ofrecer una poderosa herramienta para entender fenómenos complejos, pero su aplicación correcta depende de la precisión en el análisis y la interpretación de los datos. La independencia y el escepticismo intelectual son fundamentales en la búsqueda del conocimiento, garantizando que la ciencia sirva no solo para satisfacer nuestra curiosidad, sino para proporcionar comprensión y continuidad en nuestro viaje hacia la verdad. Al final, el llamado a la reflexión en torno a las leyes de potencia y el análisis de datos nos invita a cuestionar nuestras suposiciones y a mejorar nuestras metodologías. En un paisaje científico en constante evolución, la estadística se presenta no solo como un recurso, sino como una salvaguarda contra el pensamiento erróneo y una guía en el camino hacia una comprensión más profunda de los mecanismos del universo.
En la intersección de las matemáticas, la física y la estadística, las leyes de potencia destacan como un recordatorio de la belleza, complejidad y fragilidad del conocimiento humano.