La física contemporánea se encuentra constantemente en evolución, impulsada por descubrimientos que desafían paradigmas clásicos y abren nuevas fronteras conceptuales y tecnológicas. Entre estos avances, el estudio de los eventos topológicos en el espacio-tiempo mediante caminatas cuánticas fotónicas representa una revolución que expande nuestra comprensión de la materia, la temporalidad y la topología, con aplicaciones que prometen transformar sectores como la óptica, las telecomunicaciones y la computación cuántica. En esencia, los eventos topológicos son fenómenos donde ciertas propiedades físicas derivadas de la estructura de un sistema permanecen inalterables frente a perturbaciones, otorgándoles robustez y carácter protegido. Tradicionalmente, la topología en física se ha analizado en términos espaciales, centrada en cómo las propiedades de un material o sistema cambian a medida que sus configuraciones espaciales evolucionan. Sin embargo, la incorporación del tiempo como una dimensión activa —y no solo un parámetro pasivo— abre un nuevo horizonte: la topología en espacio-tiempo.
Las caminatas cuánticas fotónicas son una herramienta experimental y teórica ideal para explorar estos fenómenos. Basadas en la evolución stepwise de partículas cuánticas —en este caso, fotones— que atraviesan redes o redes complejas de manera controlada, estas caminatas permiten codificar estados en bloqueos sintéticos de espacio y tiempo. Al manipular estos sistemas, investigadores pueden observar cómo se desarrollan estados topológicos que no solo están localizados espacialmente, sino también temporalmente, manifestando eventos topológicos en un marco espacio-temporal. Uno de los aspectos más fascinantes que aporta esta línea de investigación es el tratamiento innovador del tiempo como una dimensión unidireccional con una «flecha del tiempo», una característica que lo distingue de las dimensiones espaciales. En relación con la topología, esto implica que los estados topológicos pueden surgir no sólo en interfaces espaciales, donde diferentes configuraciones de un sistema coexisten lado a lado, sino también en interfaces temporales, marcando cambios dinámicos a lo largo del tiempo.
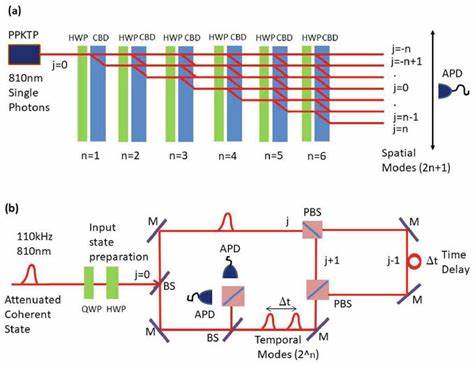
Por ejemplo, en sistemas fotónicos diseñados específicamente, al alternar parámetros como las modulaciones de ganancia y pérdida en la estructura que gobierna la caminata cuántica, se pueden crear femtopatrones donde emergen estados topológicos localizados en instantes temporales muy definidos. La experimentación moderna ha demostrado esto con éxito mediante la implementación de redes de fibra óptica acopladas que simulan estas caminatas. Utilizando moduladores y amplificadores específicos, es posible introducir dinámicas de ganancia-pérdida (no-Hermíticas) que permiten el control preciso de los llamados «gaps» de momento y energía. Los 'momentum gaps' son regiones donde los valores asociados al movimiento (el momento) presentan discontinuidades o condiciones especiales, y juegan un papel crucial en la generación de estados topológicos temporales. A su vez, la existencia simultánea de brechas en energía y momento habilita la aparición de lo que se denomina topología espacio-temporal, donde los eventos topológicos no sólo están confinados en espacio o tiempo por separado, sino en un punto específico dentro del espacio-tiempo.
Esta conjunción espacio-temporal posee características sin precedentes. La causalidad, por ejemplo, impone restricciones naturales sobre cómo se pueden excitar o influenciar estos estados topológicos; un fenómeno llamado acoplamiento suprimido por causalidad establece que un estado espacio-temporal sólo puede ser activado por una excitación presente en su cono de luz pasado, respetando así la irreversibilidad inherente a la dimensión temporal. Esta particularidad aporta una robustez adicional frente a perturbaciones y excitaciones no deseadas, un atributo muy valioso para el diseño de dispositivos ópticos y cuánticos confiables. Además, estos eventos exhiben un comportamiento singular frente a la desorden o imperfecciones, comunes en cualquier sistema físico real. Mientras que en la topología convencional el colapso de un gap energético compromete la existencia de estados protegidos, en la topología espacio-temporal la localización puede romperse parcialmente —por ejemplo, en el espacio pero no en el tiempo— dando lugar a un colapso limitado.
Esto representa una dimensión adicional de robustez topológica que podría mejorar la estabilidad de futuros dispositivos basados en estos principios. La teoría que sustenta estos fenómenos se fundamenta en modelos cuidadosamente elaborados, como la extensión temporal del modelo Su–Schrieffer–Heeger (SSH), un marco reconocido por revelar propiedades topológicas en estructuras de doble banda. Al implementar modulaciones dinámicas en sistemas cuánticos discretizados, se controla la apertura y cierre de los gaps tanto en energía como en momento, lo cual habilita la manipulación de los respectivos invariantes topológicos. Estos invariantes, de naturaleza matemática, representan números enteros que codifican el carácter topológico del sistema y predicen la aparición de estados localizados en interfaces especificadas. El avance experimental realizado mediante fibras ópticas acopladas es especialmente notable por su versatilidad y precisión.
Los pulsos de luz circulan por bucles de fibras con diferentes retardos temporales, creando effectively un espacio discreto de posiciones y tiempos para los fotones. Manipulando parámetros como el coeficiente de acoplamiento y las modulaciones en ganancia-pérdida, se puede esculpir la topología del sistema para inducir estados localizados en fronteras espaciales, interfaces temporales o incluso intersecciones espacio-temporales. Este logro no sólo tiene un impacto fundamental en la física topológica, sino que también abre la puerta a aplicaciones prácticas innovadoras. La capacidad de controlar y manipular la localización de ondas lumínicas en márgenes espacio-temporales puede revolucionar el diseño de láseres topológicos, que serían menos susceptibles a defectos o interferencias. En telecomunicaciones, la topología espacio-temporal proporciona una herramienta poderosa para el control de señales y posiblemente para la protección frente a ruidos o pérdidas.
En el ámbito de la imagen y el control de ondas, la manipulación topológica puede permitir enfoques novedosos para la mejora de la resolución o la transmisión de información en ambientes complejos. Es interesante también destacar la conexión entre estas investigaciones y la geometría fundamental del universo y otros campos como la termodinámica, donde la flecha del tiempo también juega un rol esencial. La topología espacio-temporal y sus invariantes pueden ofrecer nuevas perspectivas teóricas para entender cómo los sistemas físicos evolucionan, cómo se generan irreversibilidades y cómo se manifiestan propiedades robustas en medios dinámicos y abiertos. El camino hacia un entendimiento profundo de estos fenómenos también implica desafíos y oportunidades para futuras líneas de investigación. Por ejemplo, la generalización hacia dimensiones superiores, la integración con sistemas cuánticos más complejos e interactuantes, y el estudio del impacto de la no-Hermiticity en la robustez y la dinámica de los estados topológicos en espacio-tiempo, son áreas fértiles para seguir explorando.
Además, la implementación en otros medios físicos como átomos ultrafríos, estructuras no lineales o fluidos de superficie amplía el alcance y el impacto potencial de la topología espacio-temporal. En conclusión, los eventos topológicos en espacio-tiempo descubiertos y estudiados mediante caminatas cuánticas fotónicas representan un avance crucial en la física moderna, combinando conceptos de topología, dinámica no-Hermítica, y la naturaleza esencialmente unidireccional del tiempo. Su relevancia trasciende la teoría para situarse en el corazón de tecnologías emergentes en fotónica avanzada, procesamiento de información y tecnologías cuánticas, dejando abierta la posibilidad de nuevas formas de manipular la luz y la materia con una precisión y resistencia sin precedentes. Este campo, aún en plena expansión, ejemplifica cómo la investigación interdisciplinaria y el uso creativo de plataformas experimentales pueden desentrañar aspectos fundamentales de la realidad, al tiempo que fomentan innovaciones tecnológicas transformadoras.