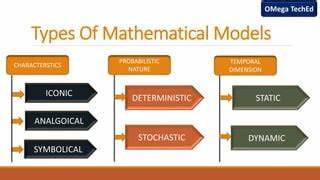
Los modelos matemáticos son herramientas indispensables en el avance del conocimiento científico y tecnológico. A lo largo del tiempo, investigadores y teóricos han desarrollado distintas maneras de conceptualizar, construir y presentar estos modelos para entender fenómenos complejos, predecir comportamientos futuros o clasificar teorías. En este sentido, se reconocen tres tipos fundamentales de modelos matemáticos: insilicación, heurística y abstracción, cada uno con características propias y aplicaciones específicas, que también se reflejan en tres modos diferentes de presentarlos: analítico, algorítmico y computacional. Comenzando por los modelos de insilicación, estos son los modelos más próximos a la realidad empírica, constituyendo una representación matemática que intenta replicar fielmente las dinámicas observadas en fenómenos físicos o naturales. Su base radica en traducir parámetros del mundo real, medibles y verificables, en ecuaciones o sistemas que permiten, mediante su resolución, pronosticar resultados futuros.
Tradicionalmente, estos modelos se presentan en un formato analítico, expresando las relaciones y leyes en forma de ecuaciones matemáticas que pueden resolverse o estudiarse directamente. Ejemplos clásicos incluyen la ecuación del movimiento de un proyectil siguiendo las leyes de Newton o la solución del espectro de un átomo de hidrógeno desde la mecánica cuántica. Sin embargo, en aplicaciones prácticas o cuando las ecuaciones se tornan demasiado complejas, la solución analítica a menudo no es factible, dando paso a la presentación computacional. Aquí, la simulación numérica y el cálculo mediante software especializado sostienen la capacidad predictiva del modelo. Civil ingenieros que evalúan las tensiones en un diseño estructural o la simulación de trayectorias para misiones espaciales son ejemplos paradigmaticos donde las insilicaciones dominan.
Lo esencial en estos modelos es el entendimiento profundo de las ecuaciones subyacentes y la confianza de que cualquier desviación respecto a las observaciones empíricas responde a características bien definidas y evaluables. Por otro lado, los modelos heurísticos representan una tipología más flexible, corriente especialmente en las ciencias sociales y biológicas, donde las variables son múltiples y el entorno no es estrictamente determinista. George Box afirmó que todos los modelos son erróneos, pero algunos resultan útiles, aludiendo precisamente a esta naturaleza de la heurística. Los modelos heurísticos frecuentemente utilizan supuestos que no tienen que ser literalmente verdaderos ni directamente comprobables desde un punto de vista empírico. Aun así, su valor reside en poder capturar patrones generales o facilitar conceptualizaciones teóricas que sirven como punto de partida para análisis o para generar hipótesis.
El desafío de los modelos heurísticos radica en encontrar un balance entre la simplicidad y la representación suficiente del sistema. Tradicionalmente, su presentación puede ser analítica, con formulaciones mediante ecuaciones o axiomas que a veces se prueban únicamente por consistencia lógica. En otros casos, adoptan una presentación algorítmica, que implica definir procedimientos o reglas formales que simulan comportamientos dentro de las teorías propuestas. Además, existe su uso en un formato computacional, común en campos como sistemas complejos o economía de la complejidad, al ser simulados en computadoras para observar comportamientos emergentes. No obstante, esta última forma puede resultar problemática, pues sin un vínculo claro entre las hipótesis y las conclusiones, el modelo puede carecer de rigor explicativo real, quedando relegado a una función meramente ilustrativa o retórica.
Finalmente, el tercer tipo de modelo se denomina abstracción y corresponde a la forma más rigurosa y general de modelado matemático, predominante en las matemáticas puras y la informática teórica. Los modelos abstractos no buscan representar fenómenos específicos, sino más bien establecer marcos conceptuales que permitan extraer conclusiones universales para cualquier sistema que cumpla determinadas premisas. Por ejemplo, la noción de máquina de Turing es un modelo abstracto que permite clasificar sistemas computacionales en términos de su capacidad y limita lo que puede ser computado en general. Las abstracciones generalmente se presentan en forma analítica o algorítmica, buscando demostrar que ciertas consecuencias se derivan necesariamente de premisas dadas, con rigurosidad matemática. Cabe destacar que no suelen servirse de simulaciones computacionales, pues el interés reside en su caracterización teórica y universal.
Este tipo de modelado es fundamental para la clasificación de teorías y la conexión entre distintas disciplinas, permitiendo, por ejemplo, testar la computabilidad o la decidibilidad dentro de campos tan diversos como la física, la biología y las ciencias sociales. Es relevante aclarar que, aunque estos tres tipos de modelos cubren múltiples necesidades y enfoques, existen otras formas de modelado fuera del ámbito estrictamente matemático. Los modelos mentales, basados en intuiciones o narrativas verbales, y los modelos físicos o experimentales, como los organismos modelo en biología, completan el panorama general de cómo se intenta comprender la realidad. Actualmente, la interacción entre las tipologías y presentaciones crece en complejidad, y nuevas áreas como el aprendizaje automático o la inteligencia artificial cuestionan y amplían esta clasificación. Por ejemplo, el aprendizaje de máquinas combina elementos computacionales y algorítmicos para generar modelos basados en datos empíricos, abriendo debates sobre si su proceso encaja en heurísticas, insilicaciones o requiere una categoría adicional.
El reto está en generar modelos que además de predecir, aporten entendimiento genuino y fundamentado. En resumen, comprender las diferencias y aplicaciones de insilicación, heurística y abstracción en el modelado matemático es fundamental para para escoger adecuadamente la metodología en función del objeto de estudio, la naturaleza del sistema y los objetivos del investigador. Reconocer los límites y fortalezas de cada tipo, así como la manera en que se presentan, garantiza un uso eficaz y crítico de los modelos matemáticos, que son piedras angulares para el avance científico en múltiples campos. Este panorama multidimensional contribuye a clarificar por qué diferentes disciplinas abordan el modelado con herramientas y criterios diversos, y cómo un modelador puede beneficiarse al conocer esta tipología para mejorar sus análisis, promover interdisciplinariedad y evitar confusiones conceptuales en la comunicación científica y tecnológica.