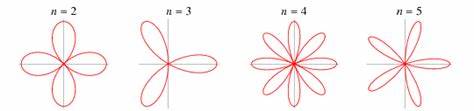
Los pétalos de rosa, con su delicada apariencia y compleja forma, han fascinado a artistas, biólogos y científicos durante siglos. Sin embargo, detrás de su belleza natural se encuentra un fenómeno matemático inusual que explica cómo se forman sus bordes enrollados y puntas afiladas. Investigadores recientes han descubierto que los rosales utilizan un tipo de retroalimentación geométrica nunca antes observada en la naturaleza para controlar el crecimiento de sus pétalos, otorgándoles esa configuración tan característica y estética. Esta innovación en la comprensión de la biología vegetal invita a explorar nuevas fronteras entre la física, la matemática y la biología del desarrollo. La forma de los pétalos de rosa no es fruto del azar ni solo de procesos biológicos tradicionales como la genética o la bioquímica.
En realidad, el fenómeno está fuertemente ligado a la mecánica del crecimiento y a cómo las células y tejidos responden a fuerzas físicas durante su desarrollo. La investigación, publicada en la revista Nature en 2025, revela que conforme el pétalo crece y empieza a curvarse hacia afuera, un mecanismo de retroalimentación mecánica regula su extensión, promoviendo que algunas zonas se doblen y formen bordes rizados y puntas agudas. Este tipo de control por fuerzas internas en el tejido es una manera eficiente para que la planta construya formas complejas sin la necesidad de instrucciones genéticas extremadamente precisas para cada detalle de su morfología. Para llegar a estas conclusiones, los científicos combinaron análisis teóricos con experimentos prácticos que usaban láminas de plástico flexibles para simular el comportamiento de los tejidos vegetales. Las simulaciones por computadora reprodujeron el efecto de crecimiento diferencial y permitieron comprobar cómo pequeñas tensiones mecánicas inducen patrones concretos de curvaturas.
El resultado fue una clara evidencia de que la forma final del pétalo emerge gracias a la interacción entre el crecimiento celular y la geometría inherente del tejido. Lo más sorprendente de este descubrimiento es que el mecanismo de retroalimentación parece ser novedoso en el mundo vivo. Los pétalos no solo responden pasivamente a su forma cambiante sino que manipulan activamente el crecimiento para adaptar su configuración, una estrategia que podría encontrarse también en otras estructuras biológicas donde la forma cumple un papel funcional indispensable, como en las hojas o alas de ciertos insectos. Desde la perspectiva de la matemática aplicada y la física, el modelo que explica la formación de los pétalos combina elementos de geometría diferencial y teoría de materiales elásticos. La superficie del pétalo es un ejemplo natural de una hoja delgada sujeta a deformaciones no uniformes, cuyas propiedades pueden analizarse mediante ecuaciones que describen cómo la curvatura y las tensiones internas evolucionan con el tiempo.
La retroalimentación mecánica actúa esencialmente como un sistema autorregulado que evita deformaciones excesivas o defectos estructurales, garantizando así la integridad del pétalo a pesar de su complejidad. Este avance abre nuevas puertas tanto para la biología como para la ingeniería. Entender cómo la naturaleza controla la forma mediante procesos físicos precisos pero flexibles puede inspirar el diseño de materiales inteligentes y estructuras adaptativas en diversos ámbitos tecnológicos. Por ejemplo, la fabricación de tejidos artificiales con capacidades similares a los pétalos de rosa podría revolucionar desde la robótica blanda hasta la arquitectura bioinspirada. Además, el hallazgo aporta información sobre la evolución de las plantas y la optimización de sus órganos para cumplir funciones específicas, como atraer polinizadores mediante formas atractivas o maximizar la exposición a la luz.
Explorar la interacción entre las propiedades mecánicas y el crecimiento celular puede ayudar a desentrañar otros enigmas de la naturaleza relacionados con el desarrollo y la adaptación. Los datos experimentales indican que la forma puntiaguda y los bordes enrollados de los pétalos no solo tienen un valor estético, sino que están directamente vinculados a funciones biológicas. Estas características pueden facilitar la repulsión de agua o la retención de polen, aumentando así la eficacia reproductiva de la planta. Entender matemáticamente estos procesos también ofrece oportunidades para mejorar prácticas agrícolas y de jardinería, potenciando el cultivo de rosas más resistentes o con formas específicas deseadas por el mercado. En conclusión, la investigación sobre la matemática inusual que da forma a los pétalos de rosa no solo resuelve un antiguo misterio natural, sino que además integra distintos campos científicos para ofrecer una visión más holística sobre cómo la vida construye sus formas.
Este descubrimiento refleja la riqueza interdisciplinaria de la ciencia actual y afirma la importancia de combinar teoría, experimentos y simulaciones para comprender fenómenos complejos. A medida que se profundice en esta línea de estudio, es probable que encontremos mecanismos similares en otros organismos, transformando nuestro entendimiento de la morfología y el crecimiento. La rosa, símbolo universal de la belleza, ahora también representa un fascinante laboratorio natural para la exploración matemática y física, un recordatorio de que la naturaleza es a la vez arte y ciencia en perfecta armonía.