El aprendizaje para una computadora consiste en transformar suposiciones iniciales erróneas en estimaciones cada vez más precisas. Comprender cómo ocurre este proceso requiere empezar con conceptos sencillos, como una línea recta, que es el fundamento de la regresión lineal y un punto de partida hacia métodos más sofisticados como el descenso del gradiente. Uno de los ejemplos más comunes y accesibles para comprender estos conceptos es el mercado inmobiliario, específicamente la relación entre el tamaño de una casa y su precio. Es un patrón intuitivo y cotidiano: casas más grandes tienden a valer más y viceversa. Aunque existe ruido y variabilidad en los datos, el patrón general revela una tendencia ascendente reconocible.
Cuando se representan gráficamente los precios en función de los metros cuadrados, observamos una dispersión con un leve ascenso, lo cual indica que la relación es continua y gradual, no categórica. Al vender una propiedad que es, por ejemplo, 1,850 pies cuadrados, podemos preguntarnos: ¿cuál es un precio justo considerando la dispersión de valores en ventas anteriores? Una manera sencilla de aproximarse es trazar a mano una línea que nos parezca ajustar bien a estos datos. Esta línea refleja un modelo simple donde el precio estimado es igual al producto del tamaño de la casa por una constante (la pendiente o coeficiente) más un valor fijo (la intersección o intercepto). Esta fórmula básica, aunque elemental, es la esencia de la regresión lineal. La pendiente representa cuánto aumenta el valor por cada unidad adicional de tamaño.
Si la pendiente es 150, entonces cada pie cuadrado adicional se valora en $150. La intersección indica el valor base, es decir, el precio estimado cuando el tamaño es cero, aunque en la práctica esto no tiene sentido físico, sí establece el punto de referencia de la predicción. El desafío radica en decidir cuál es la mejor línea para representar estos datos. No basta con elegir una línea que parezca ajustarse, sino que necesitamos una medida cuantitativa para evaluar qué tan bien una línea predice los datos que ya conocemos. Para ello, se emplea una función que calcula el error.
Este error es la diferencia entre el precio predicho por nuestra línea y el precio real de venta. Si la línea dice que una casa debería valer $350,000 pero se vendió por $375,000, el error es $25,000. Existen diferentes formas de medir estos errores. Un método simple sería sumar el valor absoluto de las diferencias, lo que da una idea clara de la desviación total. Sin embargo, este método puede ser insensible a errores mayores porque un par de errores medianos se suman igual que uno solo muy grande.
Esto puede reducir la confianza en el modelo, especialmente cuando las predicciones ocasionalmente fallan gravemente. Por esta razón, se prefiere utilizar el error al cuadrado. Al elevar al cuadrado, las desviaciones grandes se penalizan mucho más que las pequeñas, lo que favorece un modelo que evite errores grandes y mantenga consistencia. Por ejemplo, un error de $20,000 es cuatro veces peor que uno de $10,000 (y no solo el doble), mientras que uno de $50,000 pesa 25 veces más. La función que suma estos errores cuadráticos es conocida como función de costo o error cuadrático medio, y su minimización es el objetivo de la regresión lineal tradicional.
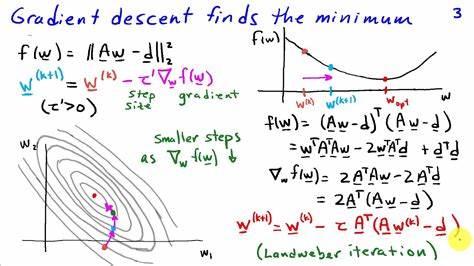
Encontrar la mejor línea implica encontrar los parámetros (pendiente e intersección) que minimizan esta función de error. Intentar probando todas las combinaciones posibles de parámetros sería imposible debido a la infinidad de valores posibles. En cambio, se visualiza el problema como un paisaje de errores donde cada punto representa una combinación específica de parámetros y su altura indica la magnitud del error. Este paisaje puede verse como una superficie lisa en el caso del error cuadrático, con una única cuenca profunda que representa el mínimo global, o como una forma mucho más irregular para otros tipos de error, como el absoluto, que puede presentar múltiples mínimos y problemas de ambigüedad. Para desplazarse por esta superficie y encontrar el mínimo, se utiliza un método iterativo conocido como descenso del gradiente.
Es una técnica que imagina moverse en dirección contraria al gradiente, o la pendiente de la función de error, para ir “bajando” hasta el punto más bajo, que corresponde al mejor ajuste. El gradiente indica la dirección en la que la función de error aumenta más rápidamente, por lo que moverse en la dirección opuesta reduce el error. Utilizando esta lógica, se ajustan paso a paso los parámetros de la línea, alejándose de los valores que producen alto error y acercándose a la combinación óptima. El descenso del gradiente es especialmente eficiente y confiable cuando se usa con funciones de error suaves y continuas, como la función de error cuadrático. Esta suavidad es crucial porque permite calcular derivadas claras y consistentes en cualquier punto, facilitando la navegación en el espacio de parámetros.
Por contraste, funciones como la del error absoluto presentan filos abruptos y puntos angulosos donde la derivada no está bien definida, lo que complica el proceso y puede llevar a soluciones ambiguas o menos estables. Este detalle matemático tiene profundas implicaciones prácticas. La elección de función de error no es una decisión trivial, sino que determina la facilidad de optimización y la estabilidad del modelo obtenido. El error cuadrático ha sido históricamente preferido porque permite usar técnicas como el descenso del gradiente de forma natural y eficaz. El descenso del gradiente, y su variante estocástica, tienen un papel fundamental en áreas avanzadas de la inteligencia artificial.
Algoritmos de aprendizaje profundo que entrenan redes neuronales dependen directamente de estos métodos para ajustar millones de parámetros y mejorar sus predicciones gradualmente durante miles o millones de iteraciones. En esencia, la regresión lineal y el método de mínimos cuadrados no solo son herramientas para ajustar una línea, sino la base de una filosofía de aprendizaje que sigue vigente. Aprender significa medir el error, interpretar su magnitud y orientación, y ajustar las suposiciones hasta minimizar esa incorrectitud. Esta aproximación matemática y computacional, nacida de problemas tan cotidianos como poner precio a una casa, ha evolucionado hasta permitir sistemas que reconocen imágenes, entienden lenguaje, conducen vehículos autónomos o diagnostican enfermedades, todos ellos siguiendo la misma lógica fundamental. Al comprender cómo una simple línea se ajusta a datos dispersos, podemos apreciar el increíble viaje desde el método de mínimos cuadrados hasta el descenso del gradiente y más allá.
Lo que parece sencillo en el papel es la base del progreso tecnológico que impulsa hoy la revolución digital y la inteligencia artificial. En conclusión, la evolución desde los mínimos cuadrados hacia el uso del descenso del gradiente ejemplifica un aprendizaje auténtico: sistemático, iterativo y basado en fundamentos matemáticos sólidos. Dominar estos conceptos es clave para entender cómo los algoritmos aprenden, cómo se entrenan los modelos predictivos y cómo la ciencia de datos transforma información en conocimiento valioso.