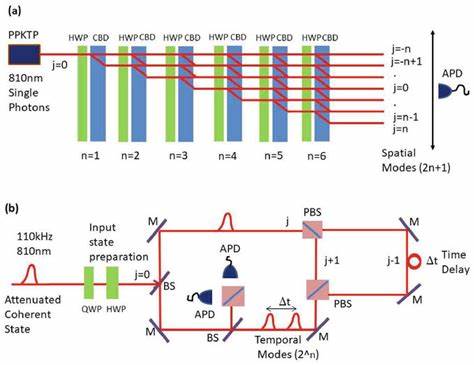
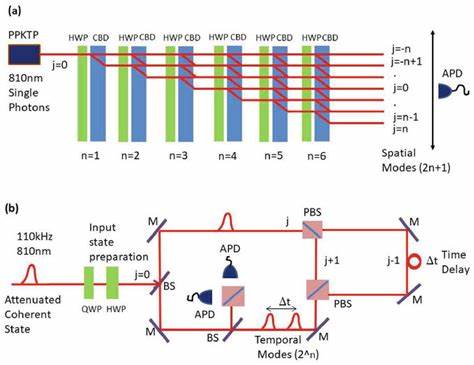
La física topológica ha transformado de manera significativa nuestra comprensión de los estados de la materia y de las propiedades fundamentales de los sistemas cuánticos. Tradicionalmente, la topología en la física ha explorado estructuras y fenómenos relacionados con las dimensiones espaciales, enfocándose especialmente en la existencia de estados protegidos por energías diferenciadas por brechas, como es el caso de los aislantes topológicos. Sin embargo, un avance reciente y revolucionario indica que el tiempo, con sus características únicas y su dirección irrestricta, puede ofrecer una nueva e intrigante dimensión para la topología, dando lugar a fenómenos que unen el espacio y el tiempo en una simbiosis que abre nuevas posibilidades tanto teóricas como experimentales. En este contexto, los paseos cuánticos fotónicos emergen como un laboratorio privilegiado para observar y manipular eventos topológicos en el espacio-tiempo. Los paseos cuánticos, en concreto los discretos implementados en sistemas fotónicos, consisten en la evolución de partículas cuánticas – para nuestro caso, fotones – sobre redes o estructuras con parámetros controlados que permiten simular diversos modelos físicos, incluyendo modelos topológicos clásicos y extendidos.
Al emplear pulsos de luz que se propagan a través de estructuras diseñadas como bucles de fibra óptica acoplados, es posible introducir dinámicas que varían en el tiempo y el espacio, generando así redes sintéticas donde las posiciones se codifican en retardos temporales y las interacciones en transformaciones ópticas específicas. Esto no solo facilita la observación de efectos topológicos espaciales sino que, gracias a la capacidad de modulación en el tiempo, se pueden crear configuraciones que manifiestan topología dependiente del tiempo e incluso combinaciones espacio-temporales. La introducción de la dimensión temporal en la topología representa un cambio paradigmático notable debido a la naturaleza irreversible del tiempo y a la presencia del denominado “flecha del tiempo”. Mientras que el espacio admite inversibilidad simétrica, el tiempo conduce irremediablemente hacia adelante. Esto implica que las propiedades topológicas que dependen del tiempo deben considerar características no hermíticas, es decir, estructuras que permiten la ganancia o pérdida de energía en el sistema y que se alejan del paradigma hermítico tradicional.
Esta cualidad fundamental contribuye a la aparición de brechas en los parámetros de momento cuántico – conocidas como “momentum gaps” – que son distintas a las clásicas brechas de energía en los sistemas espaciales. En experimentos recientes, se ha logrado diseñar y estudiar sistemas fotónicos con bucles de fibra acoplados que permiten crear y controlar tanto brechas de energía como de momento. Estos sistemas implementan versiones discreta en el tiempo de modelos topológicos clásicos como el modelo Su–Schrieffer–Heeger (SSH), incorporando además modulaciones no hermíticas a través de mecanismos de ganancia y pérdida distribuidos de modo controlado. Esta configuración aporta un grado de libertad excepcional para abrir y cerrar brechas en energía y en momento, y para explorar la topología en el ámbito temporal, espacial y de su combinación. Los estados topológicos clásicos en espacio se caracterizan por su localización en interfaces espaciales donde existe un cambio en la cantidad invariante o número topológico, emergiendo dentro de la brecha energética como estados robustos contra perturbaciones y desórdenes.
Por otro lado, los nuevos desarrollos revelan que, en presencia de brechas en el momento cuántico inducidas por la no hermiticidad, es posible definir un número topológico asociado al tiempo, que predice la aparición de estados topológicos localizados en interfaces temporales, es decir, en cambios temporales abruptos de las propiedades del sistema. Estos estados topológicos temporales exhiben características marcadamente distintas a sus análogos espaciales. En particular, dado que el tiempo es irreversible y que el sistema no es hermítico, los estados temporales tienden a crecer o decaer exponencialmente, reflejando la dinámica de ganancia o pérdida en el sistema. Esta propiedad otorga a los estados topológicos temporales una naturaleza dinámica no estacionaria, abriendo vías inéditas para manipular la propagación y la modulación de pulsos de luz en redes sintéticas. Más fascinante aún es la conjunción de los conceptos de topología espacial y temporal en lo que se denomina topología espacio-temporal.
En sistemas donde existen simultáneamente brechas tanto en energía como en momento, es posible definir invariantes topológicos que gobiernan fenómenos localizados en puntos específicos del espacio-tiempo. Estos eventos topológicos espacio-temporales corresponden a estados que no solo están confinados espacialmente sino también temporalmente, emergiendo en las intersecciones donde cambian los invariantes topológicos tanto espaciales como temporales. Este descubrimiento introduce fenómenos sin precedentes, como la supresión de acoplamiento motivada por la causalidad inherente al tiempo. En términos simples, un evento topológico espacio-temporal sólo puede ser excitado si la fuente de la excitación se encuentra dentro del cono pasado de luz de dicho evento, respetando así el principio de causalidad. Si la excitación ocurre fuera de esta región causal, la transferencia de energía al estado topológico queda bloqueada, asegurando una robustez extra frente a perturbaciones o excitaciones no deseadas.
Asimismo, la robustez de estos estados espacio-temporales frente a desórdenes exhibe comportamientos inéditos. Mientras que en la topología espacial la ruptura de las brechas energéticas suele conllevar la desaparición total de los estados protegidos, en la topología espacio-temporal es posible que la localización espacial colapse mientras que la localización temporal persiste, gracias a la capacidad de las brechas de momento de mantenerse parcialmente abiertas. Este efecto se traduce en una forma de protección topológica que es selectiva en dimensiones, abriendo nuevas perspectivas para el diseño de sistemas donde ciertas propiedades robustas se puedan conservar a pesar de imperfecciones localizadas. Desde un punto de vista experimental, la implementación en fibra óptica de estos conceptos representa un hito tecnológico y científico. Utilizando retardos precisos y moduladores de amplitud controlados electrónicamente, se pueden diseñar esquemas de acoplamiento y modulación no hermítica con gran precisión, permitiendo reconstruir con exactitud la dinámica de sistemas topológicos complejos en espacio-tiempo.
La detección a través de foto-detectores rápidos y análisis sistemáticos de la intensidad y fase de los pulsos posibilita la caracterización completa de los estados topológicos emergentes. El impacto potencial de estas investigaciones es vasto y multifacético. En primer lugar, representan un avance fundamental en la comprensión teórica y experimental de la topología extendida hacia las dimensiones tiempo y espacio-tiempo, con implicaciones en tecnologías cuánticas, fotónicas y materiales no hermíticos. En aplicación práctica, la posibilidad de controlar estados topológicos en las dimensiones temporal y espacio-temporal puede revolucionar el diseño de dispositivos fotónicos para comunicación óptica, procesamiento de señales y generación de láseres topológicos resistentes a perturbaciones. Además, la relación íntima descubierta entre la topología y la causalidad inherente al tiempo abre caminos para interconectar la física topológica con otras ramas como la termodinámica y la física de sistemas abiertos, donde el flujo irrversible del tiempo es un aspecto central.
También se vislumbran aplicaciones en sistemas cuánticos simulados, donde la manipulación del tiempo topológico puede facilitar nuevos mecanismos de control para el procesamiento de información cuántica y el estudio de fases exóticas de la materia. El desafío que se presenta a futuro consiste en ampliar la variedad de plataformas físicas aptas para explorar estos fenómenos. Si bien la implementación en bucles de fibra óptica es un excelente punto de partida, investigaciones en medios no lineales, átomos ultrafríos, metamateriales dinámicos y ondas superficiales portadoras de información están comenzando a mostrar potencial para ser escenarios fértiles en la exploración de topología en tiempo y espacio-tiempo. El desarrollo tecnológico en estas áreas fomentará la profundización del conocimiento y el surgimiento de aplicaciones que explotan la topología para la ingeniería avanzada de ondas y partículas cualquiera sea su naturaleza. En conclusión, la incorporación de la dimensión temporal en la teoría y experimentación de sistemas topológicos ha ampliado notablemente el alcance de esta disciplina, transformando el modo en que concebimos la relación entre el espacio y el tiempo en la física cuántica y fotónica.
La identificación de estados topológicos temporales y espacio-temporales mediante paseos cuánticos fotónicos evidencia no sólo la riqueza conceptual de esta nueva perspectiva sino también su viabilidad práctica. Estos hallazgos prometen desencadenar una nueva era en la física topológica, con desarrollos que podrían impactar tecnologías ópticas, computación cuántica y más allá, consolidando al tiempo como una dimensión fundamental para el control y la exploración topológica avanzada.