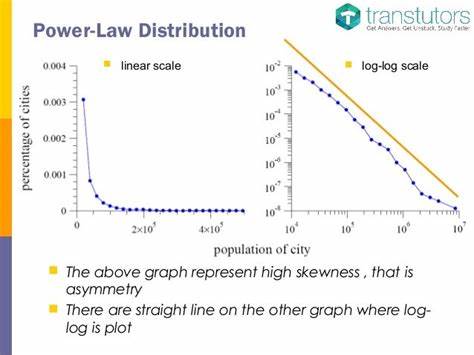
En el mundo de la ciencia, el análisis de datos es una de las actividades más fundamentales y, a menudo, subestimadas. La investigación científica no solo se basa en teorías innovadoras y suposiciones creativas, sino que, fundamentalmente, se apoya en datos sólidos que pueden confirmar o refutar esas teorías. Este delicado equilibrio entre la creatividad y la evidencia también se manifiesta en el estudio de las leyes y, en particular, en las llamadas leyes de potencia. Las leyes de potencia han emergido como patrones fascinantes en diversas disciplinas científicas, desde la geofísica hasta la biología y la economía. Una de las más conocidas es la Ley de Gutenberg-Richter, que describe la distribución del tamaño de los terremotos.
Según esta ley, la probabilidad de que un terremoto tenga una magnitud mayor disminuye de manera predecible, lo que sugiere que no hay una escala inherente para los terremotos: pueden variar enormemente en magnitud sin un límite superior. Este concepto de ausencia de escala se extiende a una variedad de fenómenos naturales y sociales. Por ejemplo, estudios han encontrado relaciones de este tipo en la distribución de grandes incendios forestales, en la cantidad de conexiones en páginas web e incluso en la distribución de la riqueza entre la población. Estas observaciones han llevado a muchos a concluir que las leyes de potencia son fundamentales para entender la naturaleza misma del universo. Sin embargo, esta fascinación por las leyes de potencia ha traído consigo una serie de desafíos y malentendidos.
La búsqueda de estas relaciones a menudo se basa en el análisis de datos que, lamentablemente, puede ser escaso o poco confiable. La historia ha demostrado que no todos los datos son iguales; algunos están marcados por errores que pueden llevar a conclusiones erróneas. Esto es lo que sucede cuando los científicos tratan de ajustar modelos de regresión a conjuntos de datos finitos; la interpretación puede ser engañosa. Una de las principales críticas es que el análisis estadístico tradicional, que asume que los errores de los datos siguen una distribución gaussiana independiente, puede no ser aplicable en esta situación. Especialmente cuando los datos son transformados logarítmicamente para identificar las supuestas leyes de potencia.
Esto puede llevar a resultados que parecen convincente a simple vista, pero que en realidad están sesgados o incluso son completamente incorrectos. Un estudio importante acometido por Aaron Clauset y sus colegas presentó un nuevo enfoque en la evaluación de estas leyes de potencia. En lugar de simplemente aplicar regresiones lineales a datos transformados, propusieron un método más riguroso que estima la probabilidad de que los datos observados puedan surgir de una ley de potencia por sí mismos. Este método se basa en el estadístico de Kolmogorov-Smirnov, que mide la mayor diferencia entre las funciones de distribución acumulativa de los datos empíricos y la ley de potencia hipotética. Lo interesante de este enfoque es que, incluso si los datos pasan la prueba inicial —es decir, si hay indicios de que podrían seguir una ley de potencia—, eso no garantiza que efectivamente lo hagan.
El análisis puede mostrar que una ley de potencia es una interpretación viable, pero también es necesario compararla con otras distribuciones, como la exponencial, que podrían resultar ser más ajustadas a los datos. Esta profundidad en el análisis es vital para evitar caer en la trampa de la sobre interpretación. Los resultados de la re-evaluación de conjuntos de datos prominentes por Clauset y su equipo encontraron que algunos datos, como los incendios forestales y la distribución de enlaces web, sí se ajustaban razonablemente bien a una ley de potencia, aunque otras formas matemáticas, como la exponencial estirada o la log-normal, ofrecían un ajuste aún mejor. Por otro lado, datos como la distribución de la riqueza mostraron no ser compatibles con una ley de potencia, lo que invita a un examen más cuidadoso de cómo percibimos y analizamos estos fenómenos. Estos descubrimientos subrayan un aspecto crítico del análisis de datos: la mente humana, con sus prejuicios y tendencias hacia ciertas interpretaciones, puede quedar atrapada en conclusiones incorrectas.
La simplicidad de una regresión lineal parece proporcionar una respuesta convincente, pero puede llevar a interpretaciones erróneas si no se usa adecuadamente. Los métodos estadísticos no son solo herramientas útiles; son salvaguardias contra el pensamiento wishful, es decir, el deseo de que algo sea cierto, independientemente de la evidencia en contrario. A medida que la ciencia avanza, es esencial que los investigadores adopten una mayor sofisticación en sus análisis. Las herramientas estadísticas deben ser empleadas no solo como un mero paso en el proceso de investigación, sino como un componente fundamental en el diseño experimental y la interpretación de resultados. La ciencia, después de todo, es un esfuerzo colectivo por comprender el mundo que nos rodea, y cada error que se presenta en el camino puede tener consecuencias duraderas.
La comunidad científica se encuentra en una encrucijada: por un lado, el impulso por buscar patrones y regularidades en datos es natural e intrínseco a la investigación. Por otro, surge la responsabilidad de hacer lo correcto con esos datos, de entender sus limitaciones y peculiaridades. Solo con este enfoque excepcionalmente crítico será posible avanzar en el conocimiento y en la validación de las teorías que explican nuestro mundo. En conclusión, el estudio de las leyes de potencia, aunque es un campo español emocionante, requiere un discernimiento cuidadoso y un enfoque estadístico riguroso. A medida que continuamos nuestras exploraciones del universo, no debemos olvidar que la calidad y la precisión en el análisis de datos son clave para convertir las conjeturas en certezas.
En este sentido, la ciencia no es un paseo por el parque, sino un camino lleno de desafíos que exigen de nosotros la máxima transparencia y rigor.