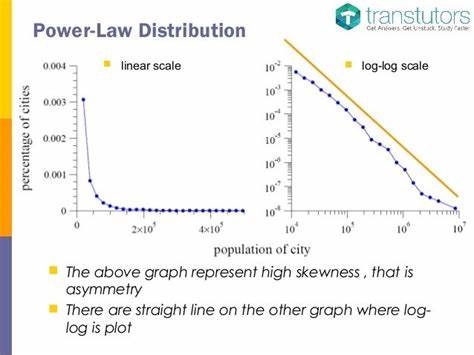
En la intersección de la ciencia y la matemática, hay un concepto fascinante que ha capturado la atención de investigadores de diversas disciplinas: la ley de potencias. Este fenómeno matemático, que describe una relación particular entre dos cantidades, ha encontrado aplicaciones en campos que van desde la biología hasta la física y la sociología. En este artículo, exploraremos los últimos artículos publicados en la revista Nature y su relación con las leyes de potencias, destacando su importancia y las implicaciones de sus hallazgos. La ley de potencias se manifiesta en la naturaleza de maneras sorprendentes. Un ejemplo clásico es la distribución de frecuencias de palabras en un lenguaje, donde la frecuencia de una palabra es inversamente proporcional a su rango en una tabla de frecuencias.
Este tipo de relación se observa en muchos otros contextos, incluyendo el tamaño de ciudades, la magnitud de terremotos, y la conectividad de redes sociales. La omnipresencia de las leyes de potencias sugiere que detrás de la complejidad del mundo, existe un orden subyacente que puede ser descrito matemáticamente. Uno de los artículos más recientes publicados en Nature Communications examina la relación entre la dinámica de la metilación del ADN y la longevidad máxima en mamíferos. Los investigadores, liderados por Steve Horvath, muestran que existe una relación inversa entre la longevidad y las tasas promedio de cambios de metilación en regiones promotoras bivalentes. Este descubrimiento no solo aporta a nuestro entendimiento sobre cómo la genética influye en la vida de los mamíferos, sino que también plantea interrogantes sobre cómo estas relaciones pueden ser modeladas a través de leyes de potencias.
El estudio de Curic et al. investiga la existencia de múltiples transiciones del estado crítico debido a anestésicos. Usando anestésicos, los autores revelan caminos múltiples desde la actividad no escalable, indicando una relación compleja entre esta actividad y el estado del participante. Este hallazgo resuena con la idea de que, en ciertos contextos, el comportamiento colectivo puede ser descrito por una ley de potencias, donde se observa que pequeñas perturbaciones pueden conducir a cambios significativos en el sistema. Un tercer ejemplo notable proviene de una investigación sobre la transmisión de enfermedades en ganado, donde Boender y Hagenaars identifican características comunes en los parámetros de transmisión espacial.
Los modelos matemáticos que describen estas dinámicas suelen seguir patrones de distribución que son característicos de las leyes de potencias. Comprender estos patrones en la transmisión de enfermedades es esencial no solo para controlar brotes, sino también para aplicar la teoría de redes en la epidemiología. Un fenómeno igualmente intrigante es la aparición de la ley 1/f en la música no humana, un estudio realizado por Jermyn et al. Este artículo explora cómo las fluctuaciones inherentes en patrones musicales se asemejan a las leyes de potencias, proporcionando una nueva perspectiva sobre cómo interpretamos la música no sólo en humanos sino en otras especies. Este cruce entre la música y la matemática nos lleva a cuestionar nuestras propias percepciones y a reconocer la música como un fenómeno que puede ser analizado matemáticamente.
La discusión sobre la universalidad de las redes escalables también ha capturado la atención de los investigadores. En un comentario importante en Nature Communications, Petter Holme plantea preguntas sobre si estas redes son raras o universales. A través de la investigación reciente sobre las distribuciones de grado en redes, se pueden hacer ajustes en la terminología para proporcionar claridad. Este debate sobre la naturaleza de las redes escalables es crucial para comprender cómo se conforman las estructuras sociales y biológicas en nuestra sociedad. Más allá de los artículos y la investigación, es esencial considerar cómo estos descubrimientos afectan a nuestro entendimiento del mundo.
Las leyes de potencias nos brindan una herramienta poderosa para modelar fenómenos complejos, permitiéndonos simplificar y predecir comportamientos en sistemas que de otra manera parecerían caóticos. Por ejemplo, al aplicar leyes de potencias a la epidemiología, los científicos pueden prever cómo una enfermedad se propagará a través de una población, lo que les permite preparar respuestas más efectivas. Además, el entendimiento de la ley de potencias puede influir en el desarrollo de tecnologías emergentes. En el campo de la inteligencia artificial y el aprendizaje automático, por ejemplo, los modelos que incorporan estos principios pueden ser más efectivos en la predicción y análisis de datos. La capacidad de identificar patrones escalables puede llevar a nuevos avances en programación y modelado de datos, creando oportunidades para la innovación tecnológica.
Sin embargo, a medida que profundizamos en el estudio de las leyes de potencias, también surgen desafíos. A menudo, los datos empíricos pueden ser ruidosos o presentar excepciones que dificultan la identificación de relaciones claras. Esto resalta la importancia de ser críticos y cuidadosos al interpretar los resultados; los científicos deben ser conscientes de las limitaciones de sus modelos y estar dispuestos a adaptarse a nuevos hallazgos. Por último, es vital mencionar que la comunicación de estos hallazgos es tan importante como la investigación en sí misma. Los artículos científicos, especialmente en revistas prestigiosas como Nature, cumplen un papel crucial en la difusión de conocimiento y en la formación de un diálogo continuo entre científicos y el público.