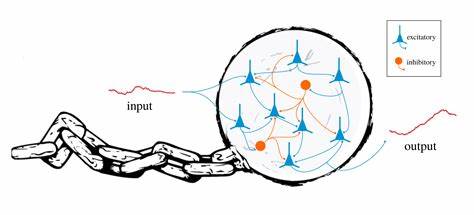
En el mundo actual, donde la biología, la neurociencia y la informática convergen, es común aceptar que las redes neuronales y los sistemas dinámicos son el fundamento para explicar la computación biológica. Desde la actividad cerebral que dirige nuestro comportamiento hasta el desarrollo celular que da forma a los organismos, las redes y sus interacciones rigen la narrativa dominante. Sin embargo, esta creencia tan extendida puede estar limitando nuestro entendimiento de cómo realmente funcionan los sistemas vivos y sus procesos cognitivos. Durante décadas, los modelos basados en estructuras de redes —ya sean redes de neuronas excitadoras e inhibidoras o redes genéticas que regulan la expresión génica— han formado el pilar del pensamiento científico en estas áreas. El enfoque parte de representar el estado de un sistema biológico mediante variables finitas que cambian en función de su interacción mutua, modeladas a menudo a través de ecuaciones diferenciales que componen un sistema dinámico.
Este marco, aunque poderoso y útil, presenta un dogma: todo sistema biológico computacional debe poder ser reducido y representado utilizando una cantidad limitada de variables con reglas definidas y constantes. Pero, ¿es esta reducción realmente suficiente? ¿Acaso no estamos ignorando aspectos fundamentales de la computación biológica por confiar ciegamente en una representación que, por su propia definición, restringe la complejidad y capacidad computacional? Para responder estas preguntas, es importante entender la diferencia crucial entre describir un sistema biológico como un sistema dinámico finito y concebir una forma de computación con un potencial mucho más amplio. Los sistemas dinámicos finitos poseen un número predeterminado de variables cuyo comportamiento evoluciona en el tiempo según ecuaciones establecidas. Si bien esta formalización puede capturar muchos procesos biológicos y físicos de manera aproximada, falla en capturar sistemas que, por su naturaleza, pueden expandir su complejidad y memoria durante la operación. Gran parte de la vida está caracterizada precisamente por el crecimiento, la adaptación y la incorporación continua de nuevas informaciones y componentes al sistema — características que desafían la idea clásica de un espacio de estado limitado y fijo.
Además, desde la perspectiva de la teoría de la computación, la capacidad de un sistema para resolver problemas complejos y realizar cómputos universales no solo depende de la cantidad de información almacenada sino también de la capacidad de modificar y extender esta memoria según los requerimientos de la tarea. Un programa de computadora típico puede, en principio, solicitar y usar memoria adicional a medida que avanza, lo que le confiere una flexibilidad y un poder computacional que los sistemas dinámicos finitos no pueden igualar. Este contraste se vuelve aún más significativo cuando se examina el concepto de computación universal, asociado comúnmente con las máquinas de Turing. Estas máquinas, y su equivalente moderno en forma de programas y lenguajes de programación, representan el límite superior de lo que se considera calculable. Mientras que una máquina de Turing puede manipular una cantidad arbitraria de memoria y adaptarse a entradas de tamaño indefinido, un sistema dinámico finito está limitado desde el inicio por su propio diseño estructural.
El debate sobre si las redes neuronales y sistemas dinámicos pueden o no alcanzar este grado de universalidad no es simplemente una cuestión teórica sino que tiene profundas implicaciones prácticas. Por ejemplo, si los cerebros biológicos o los procesos celulares estuvieran limitados a ser sistemas dinámicos finitos, entonces existiría un límite inherente a las operaciones computacionales que podrían realizar. Esto podría explicar por qué algunos problemas cognitivos o de desarrollo parecen difíciles de entender desde un punto de vista meramente dinámico o conexionista. Sin embargo, algunos estudios y modelos han sugerido que ciertos sistemas dinámicos finitos pueden simular computaciones universales. La clave de estos modelos reside en la representación de la memoria usando la precisión infinita en variables continuas, lo cual, en el mundo físico, resulta inviable debido a las limitaciones estructurales y al ruido inherente en sistemas reales.
Esta falta de estabilidad estructural descalifica, en la práctica, el uso de estos modelos para representar procesos biológicos reales. Por lo tanto, queda claro que para comprender realmente la computación en la biología y neurociencia, es necesario buscar modelos que trasciendan los sistemas dinámicos finitos. ¿Pero dónde buscar? El camino probable apunta hacia los niveles moleculares, donde conceptos como el ADN y el ARN pueden estar desempeñando roles computacionales fundamentales que todavía no entendemos a cabalidad. Desde la década pasada, ha emergido una corriente radical que postula que la memoria y el procesamiento de información pueden estar codificados no simplemente en las conexiones sinápticas, sino en la estructura y edición dinámica de moléculas dentro de la célula, especialmente en ARN y ADN. Estas moléculas pueden actuar como soportes de información capaces de crecer, modificarse y reconfigurarse en tiempo real, permitiendo una diversidad y flexibilidad computacional muy superior a la representada por las actuales redes neuronales simples.
Este enfoque está aún en desarrollo y enfrenta escepticismo, principalmente porque contraviene modelos científicos bien establecidos y requiere evidencia experimental sólida que aún es insuficiente. Sin embargo, los indicios en estudios sobre la memoria de intervalos temporales en neuronas o la respuesta adaptativa en algunos organismos apuntan hacia una computación molecular más compleja que la que los modelos clásicos permiten explicar. En un plano más amplio, la gran cantidad de ADN no codificante que existe en los organismos complica la visión tradicional. Si gran parte del genoma no produce proteínas pero tiene algún tipo de función reguladora o computacional, entonces podríamos estar frente a un modelo completamente distinto de procesamiento y almacenamiento de información en los seres vivos, un modelo que permita la expansión y modificación dinámica del espacio de estado computacional. En conclusión, el paradigma dominante basado en redes neuronales y sistemas dinámicos finitos, aunque útil para múltiples aplicaciones, puede estar impidiendo un entendimiento requerido para desentrañar los misterios de la computación biológica y cognitiva.
La ampliación del modelo hacia sistemas que contemplen el crecimiento, la expansión de memoria y la computación universal en un sentido amplio es urgente y necesaria. Descubrir cómo la vida, la cognición y el desarrollo implementan cómputos que superan las limitaciones de las matemáticas clásicas podría no solo transformar la biología, sino que también aportar valiosas inspiraciones para la computación artificial y la inteligencia artificial. A medida que la ciencia explora estas nuevas fronteras, la colaboración entre biólogos, informáticos, físicos y filósofos será esencial para construir el conocimiento que permita romper verdaderamente las cadenas impuestas por el dogma de las redes y sistemas dinámicos. La revolución computacional biológica está apenas comenzando, y quienes se atrevan a cuestionar los supuestos arraigados podrán abrir camino hacia una comprensión más profunda y completa de la vida y su capacidad infinita para procesar información.