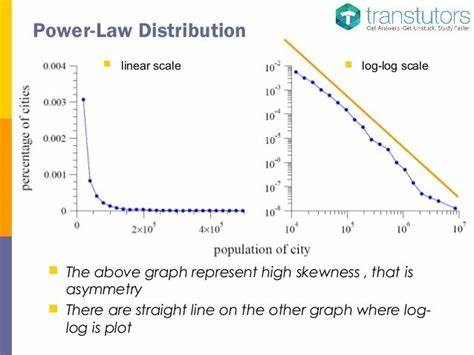
La fascinante relación de las leyes de potencia en la naturaleza En el vasto universo de la ciencia, algunas relaciones matemáticas se destacan por su capacidad para explicar fenómenos naturales complejos con elegante simplicidad. Una de estas relaciones es la "ley de potencia", un concepto que ha capturado la atención de investigadores en diversas disciplinas, desde la biología hasta la física y la sociología. En este artículo, exploraremos cómo las leyes de potencia se manifiestan en la naturaleza y su relevancia en investigaciones recientes publicadas en el Nature Portfolio. La ley de potencia describe una relación matemática entre dos cantidades, donde una de ellas varía como una potencia de la otra. En términos simples, esto significa que, a medida que se incrementa una magnitud, la otra responde en proporciones que siguen un patrón predecible.
Uno de los ejemplos más conocidos de esta ley es la distribución de frecuencia de palabras en un idioma: la frecuencia de uso de una palabra disminuye drásticamente a medida que su ranking en una tabla de frecuencias aumenta. La prevalencia de las leyes de potencia en fenómenos naturales ha llevado a numerosos estudios que buscan desentrañar sus implicancias y aplicaciones. Recientemente, varios artículos del Nature Portfolio han abordado este fascinante tema, arrojando nueva luz sobre cómo y por qué estas relaciones se manifiestan en la realidad. Uno de los estudios más destacados es el que investiga la relación entre la dinámica de la metilación del ADN y la longevidad máxima en mamíferos. Este artículo, publicado en Nature Communications, revela que existe una relación inversa entre la longevidad de las especies y el promedio de cambios en la tasa de metilación en regiones promotoras bivalentes.
Los resultados de esta investigación son cautivadores, ya que sugieren que, dependiendo del contexto de la cromatina, las tasas de metilación pueden influir en la longevidad de los organismos. Este hallazgo no solo presenta un enfoque novedoso para entender la biología del envejecimiento, sino que también resalta la conexión entre la genética y la expectativa de vida en diferentes especies. Otro artículo relevante en esta búsqueda de entendimiento es el que analiza la actividad neural bajo anestésicos, titulado "Existencia de múltiples transiciones del estado crítico debido a anestésicos". Publicado también en Nature Communications, este estudio aborda las complejidades de la actividad cerebral, sugiriendo que las desviaciones de la actividad neuronal sin escala (SF) pueden tener implicaciones significativas para la conciencia. Utilizando anestésicos, los autores descubren múltiples trayectorias desde la actividad SF, lo que indica una relación compleja entre la actividad no SF y el estado del participante.
Este tipo de investigación no solo es crucial para entender el funcionamiento del cerebro humano, sino que también plantea preguntas sobre la consciencia y su relación con fenómenos físicos. Además de las dinámicas biológicas, las leyes de potencia también se hacen presentes en otros contextos. Por ejemplo, el estudio sobre las características espectrales de la actividad humana y sus fluctuaciones intrínsecas escalares. En este artículo, los autores investigan cómo los patrones de actividad humana pueden exhibir fluctuaciones que siguen distribuciones de ley de potencia. Estas observaciones son particularmente relevantes en un mundo lleno de datos, donde el análisis de grandes volúmenes de información se vuelve cada vez más crucial.
La propagación de enfermedades también se ha convertido en un campo fértil para el estudio de las leyes de potencia. Un artículo reciente en Scientific Reports se enfoca en las características comunes en los parámetros de transmisión de enfermedades en el ganado. Este estudio no solo tiene implicaciones para la agricultura y la salud animal, sino que también aplica modelos matemáticos que pueden ayudar a predecir y controlar brotes de enfermedades. La capacidad de modelar la transmisión de enfermedades utilizando conceptos de leyes de potencia es un ejemplo claro de cómo estas leyes se aplican en el ámbito de la salud pública y la epidemiología. Incluso en el ámbito de la música, las leyes de potencia han encontrado su lugar.
Un artículo titulado "Leyes de 1/f encontradas en música no humana" investiga cómo ciertos patrones en la música, incluso en composiciones de animales, pueden seguir las leyes de potencia. Este estudio es fascinante porque sugiere que la estructura de la música, sea cual sea su origen, puede estar regida por principios matemáticos comunes. La discusión sobre las redes escalables ha sido un tema controvertido en los círculos científicos. Un artículo titulado "Raros y omnipresentes: Perspectivas sobre redes de escala libre" explora la existencia de estas redes y plantea la pregunta de si son realmente raras o universales. A través de un análisis cuidadoso de la distribución de grados en las redes, los autores presentan una perspectiva que enfatiza la complejidad de estas relaciones y el lenguaje que utilizamos para describirlas.
La discusión en torno a la teoría del "apego preferencial" y la controversia sobre si se basa en la aleatoriedad o la optimización es un reflejo de cómo las leyes de potencia pueden generar debates fértiles en la comunidad científica. A medida que los investigadores continúan explorando las leyes de potencia a través de diferentes disciplinas, es evidente que estos principios matemáticos ofrecen un marco poderoso para entender la naturaleza. Desde la biología hasta la sociología, pasando por la física y la música, las leyes de potencia proporcionan una herramienta valiosa para modelar y predecir comportamientos complejos en sistemas diversos. En conclusión, el estudio de las leyes de potencia revela la profunda interconexión de muchos fenómenos en nuestro mundo. Los artículos recientes del Nature Portfolio no solo destacan investigaciones novedosas en este campo, sino que también muestran cómo estas relaciones pueden tener aplicaciones prácticas y teóricas significativas.
A medida que la ciencia avanza, la exploración de estas maravillas matemáticas seguirá siendo un área de estudio emocionante, prometiendo nuevas revelaciones sobre la naturaleza y sus muchos misterios.