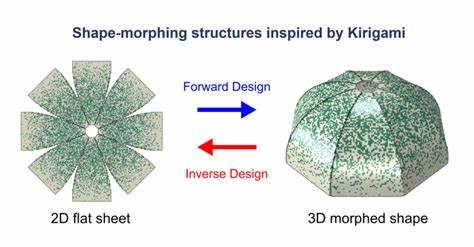
La capacidad de transformar formas y topologías de superficies cerradas representa un desafío apasionante y de gran relevancia en el ámbito de la ingeniería de materiales y estructuras. Tradicionalmente, el estudio de morfología de superficies se ha centrado en superficies abiertas o en transformaciones que parten de formas planas hacia formas curvas. Sin embargo, el cambio entre configuraciones cerradas es un terreno menos explorado debido a la complejidad inherente de mantener la integridad geométrica y mecánica de un objeto totalmente cerrado, una condición que implica restricciones más estrictas en comparación con las superficies abiertas. La reciente integración innovadora de las técnicas japonesas ancestrales de origami y kirigami ha irrumpido como una solución efectiva para superar estas barreras. Mientras que el origami se basa en plegados precisos alrededor de líneas de pliegue dentro de una superficie plana, aportando control y precisión, el kirigami incorpora cortes estratégicos en el material para otorgar grados adicionales de libertad y promover deformaciones más complejas.
Esta sinergia permite diseñar estructuras ensambladas con paneles rotacionales que combinan ambos principios para lograr una versatilidad y reconfiguración hasta ahora no alcanzadas en forma estable. Un aspecto crítico en este avance es la morfología bistable de superficies cerradas. Las estructuras resultantes pueden existir establemente en dos configuraciones distintas sin necesidad de energía constante, permitiendo la transformación entre formas muy diferentes con estímulos mínimos. Por ejemplo, un ensamblaje ori-kiri puede cambiar de manera reversible entre un cubo compacto y una esfera desplegada, o incluso alterar su topología fundamental al convertir una esfera (genus-0) en un toro (genus-1), es decir, pasando de una forma sin huecos a una con uno. Este proceso de transformación implica la armonización de movimientos alrededor de dos tipos de ejes: los pliegues origami accionados casi tangencialmente a la superficie cerrada y las bisagras kirigami orientadas perpendicularmente, que permiten la rotación entre paneles y la apertura de los cortes.
Dichos movimientos combinados otorgan a las estructuras un enorme rango de deformaciones mientras mantienen una coherencia espacial rigurosa para preservar un espacio interior cerrado o semi-cerrado según el diseño. Desde un punto de vista topológico, una superficie cerrada sin fronteras puede dividir el espacio tridimensional en un interior y exterior definidos. Esto cobra especial importancia para aplicaciones que requieren encapsulamiento, protección y modulación funcional del contenido interno. La habilidad para modificar la topología, por ejemplo creando un agujero en la superficie al lograr una transición esfera-toro, abre espacios para dispositivos inteligentes, contenedores adaptativos, o estructuras con conductos internos configurables. El desarrollo metodológico se fundamenta en un proceso de diseño en dos etapas para asegurar la compatibilidad geométrica y la estabilidad mecánica.
El primer paso aborda la optimización de la distribución de vértices y conexiones de paneles, permitiendo simular la transformación como un sistema con junta esféricas que ofrecen alta libertad de movimiento, pero aún sin restricciones totalmente definidas. Esta optimización busca preservar congruencia entre los estados compactos y desplegados, garantizando que los paneles se correspondan adecuadamente entre ambas configuraciones. Tras este logro, la segunda etapa consiste en reducir los grados de libertad mediante la sustitución de dichas juntas por bisagras con eje de rotación especificado, logrando que el sistema sea cinemáticamente determinado y, por ende, físicamente estable en dos estados de mínima energía. Este procedimiento logra que las estructuras pasen de un mecanismo con infinitas vías de movimiento a un dispositivo con dos configuraciones estables y una barrera energética para la transición entre ellas. La validación experimental se materializa a través de prototipos impresos en 3D, fabricados con precisión para reproducir los paneles y bisagras con ejes cuidadosamente orientados.
En estas muestras físicas, la transición entre las distintas formas cerradas es demostrable, y se evidencian comportamientos bistables consistentes con los predichos en simulaciones. Más allá del cambio de forma, esta tecnología permite modificar la escala de las superficies cerradas, posicionado un conjunto de paneles que escalan uniformemente entre dos radios distintos de esferas. Esta característica dota de una versatilidad adicional para aplicaciones que requieran cambio dimensional sin alterar la configuración básica. El análisis de las métricas geométricas como el radio vectorial desde el centroide, los ángulos de rotación en bisagras y pliegues, y las energías asociadas a deformaciones de estiramiento y rotación, permiten comprender detalladamente el proceso de transformación y las singularidades que surgen. Resulta notable la diferencia entre casos como la simple expansión esférica y la compleja transformación topológica esfera-toro en donde la heterogeneidad de las deformaciones es mucho mayor, lo que se refleja en los perfiles energéticos y angulares.
Una de las ventajas del enfoque ori-kiri es su aplicabilidad a formas irregulares y libres, permitiendo incluso la creación de transformaciones entre geometrías asimétricas o naturales, como la transición de una esfera a una forma ovoide o una forma inspirada en objetos cotidianos con curvas complejas. Esta flexibilidad asegura que el método no está limitado a formas regulares y abre la puerta a diseños personalizados y adaptativos. Entre las potenciales aplicaciones prácticas de esta tecnología se encuentran los metamateriales reconfigurables, estructuras blandas en robótica, dispositivos de encapsulado y liberación controlada, sistemas de filtración con permeabilidades ajustables y componentes con rigidez variable. Por ejemplo, la posibilidad de cambiar la rigidez y la permeabilidad de la estructura a voluntad mediante la transición de formas, puede resultar en empaques inteligentes, escudos adaptativos frente a radiación, o estructuras con dinámica de vibración modulada. A pesar de los avances, existen desafíos importantes, tales como la fabricación de piezas unitarias integradas con bisagras internas que mantengan la orientación precisa necesaria para la bistabilidad.
Los experimentos realizados con materiales impresos en TPU demuestran que, sin soporte interno adicional, la pérdida de orientación de bisagras reduce la calidad del cambio estable. Por ende, soluciones como anillos rígidos internos o bloqueos en zonas específicas resultan esenciales para mantener el comportamiento esperado. El rigor matemático y computacional detrás de este trabajo se basa en parametrizaciones cuidadosas de las superficies mediante mapeos UV, asignación de diagonales para activar máscaras de plegado, y formulaciones de optimización que equilibran apertura y cerramiento de los paneles. Además, el análisis de cinemática y estabilidad asegura que las soluciones propuestas no solo sean teóricas sino también realizables y funcionales. Este enfoque abre nuevas perspectivas para el diseño de estructuras que pueden cambiar su arquitectura espacial y funcionalidad de forma controlada y reversible, permitiendo la manipulación tanto de la forma como de la topología del objeto, lo que es un hito significativo en la ingeniería de superficies y metamateriales.
En resumen, la integración de origami y kirigami para la transformación de superficies cerradas contribuye a superar limitaciones históricas en la morfología de estructuras complejas, habilitando no solo cambios de forma sino también de topología, con aplicaciones que abarcan desde la robótica blanda hasta la protección y el control adaptativo en materiales funcionales. La capacidad para diseñar mecanismos con bistabilidad y control cinemático abre un amplio abanico de posibilidades para futuros desarrollos en ciencias de materiales, ingeniería mecánica y diseño innovador.