La estimación del tiempo necesario para completar una tarea es una pieza fundamental en la gestión de proyectos, especialmente en el ámbito tecnológico y de desarrollo de software. Sin embargo, es también una fuente recurrente de frustración para muchos equipos, ya que rara vez las tareas terminan dentro del plazo esperado. Este fenómeno, popularizado por la Ley de Hofstadter, afirma tristemente que las cosas siempre llevan más tiempo del previsto, incluso cuando se considera esa misma ley. ¿Por qué sucede esto y cómo podemos conquistar este desafío aparentemente ineludible? Para entender el problema, es crucial analizar cómo se generan y comunican las estimaciones. En muchas organizaciones, a pesar de contar con equipos altamente talentosos y experimentados, las fechas entregadas terminan siendo tomadas como compromisos sin matices.
Unas cifras que originalmente pretendían ser aproximaciones terminan siendo divulgadas como certezas a clientes y departamentos, generando expectativas difíciles de manejar y daños en la confianza cuando no se cumplen. Un error común radica en cómo se interpreta la estimación. Cuando un equipo de desarrollo propone, por ejemplo, seis meses para entregar un producto mínimo viable, el área de marketing o ventas puede entender que ese plazo es firme y absoluto. Sin embargo, en realidad, el tiempo estimado corresponde con frecuencia a una mediana estadística —el punto donde hay un 50% de probabilidad de terminar antes y un 50% después— y no implica ninguna garantía sobre el tiempo máximo o seguro de entrega. Este malentendido puede generar tensiones internas y externas que dañan tanto la imagen de la empresa como la dinámica de trabajo del equipo técnico.
Además, suele suceder que incluso los desarrolladores mismos no internalicen completamente la incertidumbre inherente a sus estimaciones. La naturaleza de algunas tareas, especialmente aquellas que involucran innovación o refactorización profunda, supone variables imprevisibles que se descubren solo durante el desarrollo. Este efecto es conocido como “descubrimiento de alcance” y difiere del tradicional “deslizamiento de alcance” relacionado con añadidos posteriores no contemplados inicialmente. A pesar de las múltiples técnicas implementadas en la industria para mejorar la precisión de las estimaciones —como story points, planificación con Fibonacci, y metodologías ágiles— la dificultad persiste. La solución, según estudios recientes y análisis detallados basados en datos rigurosos, no es simplemente ajustar números o usar un método mágico, sino entender la distribución probabilística que subyace bajo cada estimación.
Al analizar una gran cantidad de tareas con estimaciones iniciales, y luego observar sus tiempos reales de finalización, se ha encontrado un patrón revelador: las desviaciones siguen consistentemente una distribución lognormal. Este tipo de distribución describe situaciones donde los resultados están influenciados por la multiplicación de varias variables aleatorias, en contraste con la suma simple que genera distribuciones normales o gaussianas. En la práctica, esto refleja que el proceso para completar una tarea técnica no es lineal ni predecible con exactitud simplemente sumando tiempos. El desarrollo de software sigue caminos inciertos, donde enfrentarse a obstáculos imprevistos, corregir errores, validar funcionalidades y coordinar agrupaciones múltiples de trabajo generan variabilidad multiplicativa. Esta comprensión cambia la forma en que debemos interpretar y comunicar las estimaciones.
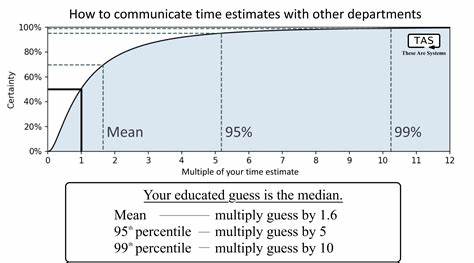
Los desarrolladores tienen un buen sentido para calcular la mediana —el tiempo con la probabilidad 50%— pero rara vez esto es lo que se espera escuchar. Cuando un encargado de producto o marketing pregunta por un plazo, suele buscar un número que garantice con alta certeza la entrega, a menudo una probabilidad del 90% o 99%. Es decir, un tiempo considerablemente mayor que la mediana para cubrir la cola larga de imprevistos. Igualmente, para la planificación interna dentro del equipo, el promedio o la media puede ser la cifra más útil para distribuir la carga de trabajo entre sprints, ya que asume que el tiempo extra de algunas tareas puede compensarse con otras terminadas antes de lo previsto. Por lo tanto, comunicar una única estimación numérica sin el contexto adecuado es una compresión excesiva que provoca malos entendidos y falsas expectativas.
Por esta razón, es recomendable acompañar las cifras con explicaciones sobre el nivel de confianza que representan y si se trata de una mediana, una media o un percentil superior que refleje un margen de seguridad. Además, esta perspectiva permite diseñar multiplicadores para ajustar los tiempos según el nivel de riesgo tolerado en la comunicación. Por ejemplo, si el tiempo estimado es “m”, la media real suele multiplicarse por 1.6, según la fórmula derivada del comportamiento lognormal. Para obtener un tiempo con 99% de confianza, sería necesario multiplicar por un factor aún mayor, reflejando los escenarios menos favorecidos que aunque rara vez ocurren, no son imposibles.
El impacto de aplicar una visión probabilística correcta va más allá de la predicción en sí. También promueve un ambiente de trabajo más saludable, ya que se reducen las presiones por cumplir plazos irreales y se mejora la confianza entre todas las partes involucradas. La clave está en educar a los interesados para que comprendan que la estimación es una predicción con un grado de incertidumbre, no una garantía infalible. Por último, es importante destacar que esta modelo funciona particularmente bien para proyectos tecnológicos innovadores o con un alto componente de exploración interna y desarrollo desde cero, donde las dependencias y complicaciones tienen una estructura compleja y fractal. No es igual para tareas rutinarias, repetitivas o procesos que dependan de factores externos con tiempos regulares, como la adquisición de insumos con plazos fijos.
En conclusión, conquistar la Ley de Hofstadter requiere cambiar cómo entendemos la estimación de tareas, pasando de una visión simplista a una basada en probabilidades y en una comunicación clara que se ajuste a las necesidades de cada interlocutor. Esto implica validar las intuiciones mediante datos, utilizar herramientas estadísticas como la distribución lognormal para describir incertidumbres, y adaptar las cifras a diferentes usos según el riesgo que se está dispuesto a asumir. Al hacerlo, tanto equipos de desarrollo como gerencia y clientes pueden alcanzar niveles más realistas, efectivos y satisfactorios en la planeación y ejecución de proyectos tecnológicos.