La física moderna se encuentra en una etapa fascinante donde las fronteras entre espacio, tiempo y topología convergen para dar lugar a fenómenos que redefinen nuestra comprensión fundamental del universo. Entre estos avances, el estudio de los eventos topológicos en el espacio-tiempo mediante caminatas cuánticas fotónicas abre nuevas vías para explorar cómo la luz puede manipularse y controlarse con una precisión sin precedentes, ayudando a sentar las bases para tecnologías futuras en campos tan diversos como la comunicación y la imagenología. Para comprender la magnitud de este fenómeno, es esencial remontarse a los cimientos de la física topológica, rama que ha sido crucial para entender materiales con propiedades únicas tales como los aislantes topológicos. Estos materiales presentan estados en sus superficies que, gracias a su naturaleza topológica, son resistentes a defectos o perturbaciones, permitiendo conductividad sin pérdidas significativas por retrodispersión. Tradicionalmente, la topología se ha desarrollado y aplicado considerando principalmente las dimensiones espaciales, donde las fronteras en el espacio determinan la aparición de estos estados protegidos.
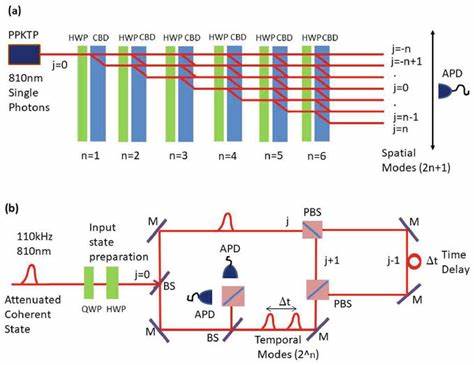
Sin embargo, el tiempo aporta una dimensión de naturaleza profundamente distinta debido a su unidireccionalidad, conocida como la “flecha del tiempo”. Esta asimetría temporal tiene implicaciones fundamentales que desafían las nociones clásicas de simetría y reciprocaidad presentes en el espacio, lo que conduce a fenómenos topológicos peculiares solo observables cuando el tiempo se incorpora de manera directa en el análisis. En particular, la introducción de la topología temporal permite definir estados que están localizados no espacialmente, sino en intervalos específicos de tiempo, dando origen a nuevas categorías de fenómenos que cambian las posibilidades de manipular ondas y partículas. El estudio de caminatas cuánticas fotónicas otorga un marco experimental ideal para explorar estas ideas. En este contexto, las caminatas cuánticas se refieren a la propagación controlada de partículas de luz a través de un entramado ordenado de caminos, que pueden ser manipulados para simular las complejidades de modelos topológicos clásicos y nuevos.
Mediante la implementación en fibras ópticas acopladas con retardos temporales y modulaciones en ganancia y pérdida, es posible construir un equivalente sintético de un sistema con dimensión espacio-tiempo discreta, permitiendo observar directamente la dinámica de estos estados topológicos tanto en el espacio como en el tiempo. Uno de los modelos base para entender estos sistemas es la adaptación temporal del modelo de Su–Schrieffer–Heeger (SSH), que originalmente describía modos en cadenas de polímeros con acoplamientos alternados. Con la introducción de un módulo que representa ganancia y pérdida de forma periódica en el tiempo, el sistema se vuelve no hermítico, lo que es fundamental para la aparición de brechas en el espectro conocidas como brechas de momento. A diferencia de las brechas energéticas espaciales que conducen a estados evanescentes en el espacio, estas nuevas brechas de momento están asociadas a estados que crecen o decaen en el tiempo, una característica intrínseca a su topología temporal. Los experimentos con estos sistemas revelan que cuando se crea un cambio abrupto en la topología temporal, por ejemplo, mediante la variación de la intensidad de la ganancia y pérdida a través del tiempo, aparecen estados lumínicos que se localizan precisamente en la interfaz temporal donde cambia el invariante topológico temporal.
Estos estados no son estáticos y, por su naturaleza no hermítica, pueden crecer o decaer, lo que implica que requieren un tratamiento diferente al de la topología espacial tradicional. El siguiente gran paso ha sido transcender la separación clásica entre topología espacial y temporal, definiendo lo que se conoce como topología espacio-temporal. En este escenario, se manipulan parámetros para abrir brechas simultáneamente tanto en espacio como en tiempo, lo que genera eventos topológicos que están localizados en un punto específico del espacio-tiempo. Estos eventos son singulares porque representan estados que no solo están confinados en una región espacial sino también en un instante temporal bien definido. La importancia de estos eventos espacio-temporales va más allá de la mera observación experimental.
Desde el punto de vista teórico, representan un nuevo paradigma donde las leyes de la causalidad y la no hermiticidad juegan papeles esenciales en la formación y protección de estados topológicos. Por ejemplo, se ha observado que la posibilidad de excitar un estado topológico en un evento espacio-temporal depende estrictamente de si la fuente de excita está dentro del cono de luz pasado del evento, una manifestación directa de la causalidad inherente al tiempo. Esto da lugar a la sorprendente capacidad de suprimir el acoplamiento hacia estos estados cuando la excitación está fuera de este cono, confiriendo a estos sistemas un nivel superior de robustez y selectividad. Otro punto innovador tiene que ver con la robustez frente a desorden y perturbaciones. Mientras que en sistemas topológicos convencionales la destrucción de brechas energéticas suele implicar la desaparición completa de los estados protegidos, en estos eventos espacio-temporales la destrucción puede ser parcial, afectando solo la parte espacial y dejando intacta la localización temporal.
Esto introduce un concepto novedoso de colapso limitado que añade una nueva dimensión a la protección topológica de estados y abre la puerta para aplicaciones donde la estabilidad a largo plazo es crítica. Las aplicaciones potenciales de estos descubrimientos son vastas. En la óptica y la fotónica, la capacidad de controlar y moldear las ondas de luz tanto en espacio como en tiempo con propiedades topológicamente protegidas puede revolucionar la imagenología avanzada, mejorando la resolución y reduciendo el ruido, o en las comunicaciones ultrarrápidas, donde la manipulación de pulsos de luz puede aprovecharse para enviar información de manera eficiente y con menos interferencias. Además, la creación de láseres topológicos que se benefician de estas propiedades podría llevar a dispositivos más robustos y eficaces en entornos difíciles. También se vislumbran vínculos con otras áreas fundamentales de la física.
Por ejemplo, la relación entre la topología temporal y conceptos termodinámicos relacionados con la flecha del tiempo sugiere nuevas perspectivas sobre procesos irreversibles, disipación y la formación de orden. En sistemas quirales y no hermíticos más generales, esta investigación abre caminos para explorar nuevos estados de la materia y fenómenos no convencionales. El enfoque experimental basado en el uso de fibras ópticas acopladas y moduladores de ganancia y pérdida ilustra la versatilidad y el control que se puede alcanzar. La capacidad de crear un sistema con dimensiones discretas en espacio y tiempo y manipular in situ los parámetros esenciales ha permitido observar directamente estos fenómenos de frontera temporal y espacio-temporal, un logro que hará avanzar notablemente los estudios en materia de simulación cuántica y topología dinámica. En resumen, la combinación de caminatas cuánticas fotónicas con el análisis de topologías que incluyen la dimensión temporal y el espacio-tiempo introduce un nuevo marco conceptual y experimental para la física moderna.
Este trabajo no solo expande el conocimiento teórico sobre estados topológicos y su dinámica sino que sienta las bases para que futuras tecnologías aprovechen estas propiedades inusuales y resistentes, transformando la forma en que entendemos y utilizamos la luz, e influyendo en sectores tecnológicos clave a nivel global.