Los nudos ópticos representan una fascinante intersección entre la topología matemática y la física de la luz. Estos objetos tridimensionales, formados por líneas de singularidades de fase en campos ópticos, han capturado la atención de científicos e ingenieros, principalmente debido a su potencial para revolucionar áreas como las comunicaciones ópticas, la metrología y la fabricación micro y nanoestructurada. Sin embargo, uno de los grandes retos para su aplicación práctica es la influencia de la turbulencia atmosférica, que tiende a distorsionar las propiedades del haz óptico, provocando pérdidas en la estabilidad de la estructura topológica de estos nudos. Comprender la estabilidad de los nudos ópticos en medios turbulentos es fundamental para avanzar en su uso en entornos reales, como las comunicaciones a larga distancia por aire abierto o la exploración remota. Los conceptos topológicos aplicados a la luz han evolucionado de áreas puramente matemáticas o teóricas hacia aplicaciones en óptica clásica y cuántica.
Un nudo, en términos matemáticos, es la incrustación de un círculo en un espacio tridimensional que no puede deshacerse sin cortar o permitir que las líneas se crucen entre sí. Al trasladar esta idea a los campos ópticos, las singularidades de fase — puntos con intensidad cero donde la fase no está definida — pueden enlazarse formando líneas cerradas que se entrelazan en formas nódicas, como el famoso nudo trébol o el enlace Hopf. La creación de nudos ópticos se logra mediante la superposición controlada de modos laguerre-gaussianos (LG), cada uno caracterizado por índices radiales y azimutales que determinan su distribución espacial y momento angular orbital. En condiciones ideales, sin perturbaciones, es posible crear campos donde las líneas nodales forman nudos específicos cuya topología está determinada por invariantes como el número de cruces. Sin embargo, cuando estos haces atraviesan medios reales, como la atmósfera, la naturaleza fluctuante del índice de refracción debida a la turbulencia térmica y convectiva distorsiona la propagación de la luz.
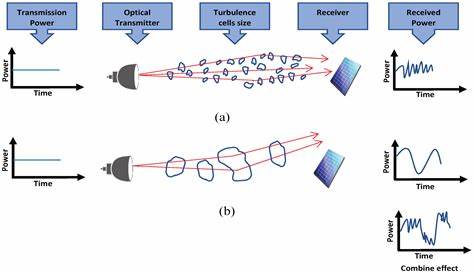
Estas perturbaciones afectan tanto la amplitud como la fase del campo, poniendo en riesgo la conservación de la estructura nódica inicial. La turbulencia atmosférica es un fenómeno universal y complejo que afecta la propagación de la luz en varias escalas, desde movimientos microscópicos hasta patrones macroscópicos. En óptica, los efectos más relevantes son la dispersión del haz (beam wandering), la fluctuación rápida de la intensidad (scintillation) y las distorsiones del frente de fase. El modelo de Kolmogorov ha servido como la base para describir estadísticamente estos efectos y proporcionar herramientas para simularlos y entender su influencia sobre los haces ópticos. Mediante la implementación de pantallas de fase que simulan las variaciones rápidas y aleatorias del índice de refracción, es posible recrear en laboratorio las condiciones de un canal turbulento controlado.
Estudios recientes han demostrado que, en regímenes de turbulencia débil, la estructura topológica de los nudos ópticos puede preservarse. Es decir, el nudo inicial — por ejemplo, un trébol — continúa existiendo con el mismo número de cruces de las líneas nodales a pesar de las pequeñas perturbaciones. Sin embargo, al aumentar la intensidad de la turbulencia, la probabilidad de que ocurran eventos de reconexión y ruptura aumenta, lo que conduce a transformaciones en la topología. Por ejemplo, un trébol puede evolucionar hacia un enlace Hopf o incluso deshacerse en una estructura sin nudos conocida como 'unknot'. Estos eventos no implican que el campo pierda toda su coherencia, sino que la configuración espacial y la interrelación entre los modos LG se alteran, afectando directamente la configuración del nudo.
Las reconexiones topológicas observadas en nudos ópticos tienen paralelos en otras áreas de la física, como en la dinámica de vórtices en superfluidos descrita por la ecuación de Gross-Pitaevskii. En estos sistemas, nudos de vórtices se unen, reconectan y separan con el tiempo, mostrando que a pesar de las leyes topológicas, la estabilidad en sistemas dinámicos y perturbados es limitada. Este paralelismo sugiere que la visión matemática estricta de la invariancia topológica debe ser complementada con consideraciones físicas y dinámicas para entender y predecir el comportamiento en aplicaciones reales. Frente a estos desafíos, se están desarrollando métodos para optimizar la construcción inicial de los nudos ópticos y maximizar su resistencia frente a la turbulencia. Una estrategia clave ha sido ajustar los coeficientes de amplitud de cada modo LG que constituyen el nudo.
Mediante algoritmos de optimización numérica, es posible espaciar mejor las singularidades de fase en el espacio tridimensional, evitando que las líneas nodales queden demasiado cercanas y susceptibles a la fusión o desconexión causadas por las distorsiones turbulentas. Esta técnica ha mostrado resultados prometedores, permitiendo preservar una mayor proporción de nudos originales bajo niveles de turbulencia más elevados. Otro aspecto relevante es el contraste en amplitud alrededor de cada singularidad. Singularidades en campos con contraste alto tienden a ser más resistentes al desplazamiento causado por turbulencia, lo que implica menor recorrido errático (wandering) y mayor estabilidad en la forma nodal. Por lo tanto, optimizaciones que incrementen este contraste pueden resultar en estructuras nódicas más robustas sin sacrificar la calidad del haz.
Las aplicaciones prácticas de estas investigaciones son vastas y de gran impacto. En comunicaciones ópticas cuánticas y clásicas, el uso de nudos ópticos como portadores de información abre la puerta a códigos topológicos complejos que pueden superar algunas limitaciones impuestas por el ruido y las distorsiones. Además, la fabricación de microestructura tridimensional usando haces con nudos optimizados podría mejorar la precisión y confiabilidad en la producción de dispositivos fotónicos y biomédicos. En metrología, la detección y monitorización de turbulencia atmosférica mediante análisis de la estabilidad de nudos permitiría desarrollar sensores avanzados para la predicción meteorológica o sistemas de navegación aérea más seguros. La experimentación en este campo combina interferometría de alta precisión y tecnologías de modulación espacial de luz, como los moduladores espaciales de luz (SLM), para generar y analizar los campos nodales.
Además, cámaras CMOS de alta resolución y técnicas de recuperación de fase permiten reconstruir y visualizar en tres dimensiones la evolución de las singularidades durante la propagación en atmósferas turbulentas simuladas o reales. La combinación con simulaciones numéricas, usando múltiples pantallas de fase que representan la escala y fuerza de la turbulencia, facilita el estudio sistemático y la validación de los métodos de optimización. A pesar del progreso, la clasificación tradicional de nudos basada en invariantes simples como el número de cruces puede no ser suficiente para describir cabalmente la complejidad de los nudos ópticos en condiciones turbulentas. Dado que las estructuras tridimensionales se deforman sin perder completamente su identidad visual, se han sugerido criterios alternativos basados en la forma global y la similitud geométrica que podrían proporcionar una mejor correspondencia con las propiedades físicas relevantes y su aplicabilidad en comunicaciones y procesamiento de la información. Los retos futuros incluyen la incorporación de modos LG adicionales en la composición del nudo para mejorar la estabilidad, el desarrollo de algoritmos de corrección adaptativos que respondan en tiempo real a las perturbaciones del medio y la exploración de nuevas bases de modos estructurados que puedan exhibir mayor resiliencia.
También se abre la posibilidad de combinar estas estructuras con técnicas de corrección adaptativa de óptica y aprendizaje automático para anticipar y compensar los efectos turbulentos. La relevancia de estos estudios trascenderá la óptica, afectando campos como la física de condensados de Bose-Einstein, dinámica de fluidos y óptica cuántica, donde los nudos y enlaces juegan un papel esencial en la descripción de estados y fenómenos complejos. Así, la comprensión profunda de la estabilidad de nudos ópticos en medios turbulentos contribuirá no solo a la ciencia básica sino también a la ingeniería de tecnologías disruptivas que aprovechen la topología para transportar y manipular información con mayor eficiencia y fiabilidad. En suma, la estabilidad de los nudos ópticos en la turbulencia atmosférica es un tema que conjuga teoría, experimentación y aplicaciones prácticas con enorme potencial transformador. Los avances en optimización de modos, técnicas de medición y modelado físico de la turbulencia permiten hoy comprender mejor los límites y oportunidades de estos sistemas topológicos en la vida real.
Mientras que la turbulencia representa un obstáculo natural y desafiante, también impulsa la innovación para garantizar que las propiedades topológicas de la luz puedan ser aprovechadas en el mundo complejo en que vivimos.