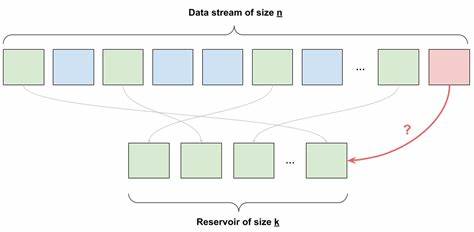
En un mundo cada vez más dominado por el flujo constante de datos, seleccionar muestras representativas de información se ha convertido en un desafío dosificado por la rapidez y el volumen. Cuando se trata de analizar o almacenar datos provenientes de un stream infinito o de tamaño desconocido, técnicas tradicionales de muestreo pierden efectividad o se vuelven inviables. Reservoir Sampling surge como una respuesta ingeniosa y eficiente a este problema, ofreciendo una solución que no requiere conocer de antemano el tamaño total del conjunto de datos y que asegura que cada dato tenga igualdad de oportunidades para ser seleccionado. Lo fascinante de Reservoir Sampling es su simplicidad conceptual combinada con una base matemática sólida que solo requiere operaciones aritméticas básicas como multiplicación, división y resta. A diferencia de métodos que dependen de mezclar o acceder directamente a posiciones específicas en un conjunto completo, esta técnica trabaja con los datos a medida que van llegando, almacenando un número fijo de elementos en una especie de depósito o “reservorio”.
Este enfoque permite mantener una muestra justa y representativa sin necesidad de un almacenamiento excesivo, un aspecto clave cuando se gestionan grandes volúmenes o flujos en tiempo real. Para ilustrar la necesidad de Reservoir Sampling, pensemos en el ejemplo clásico de seleccionar cartas de una baraja. Si conocemos la totalidad y tamaño del mazo, elegir un conjunto de cartas al azar es sencillo y justo, ya sea mezclando o eligiendo índices aleatorios. Sin embargo, ¿qué sucede cuando las cartas aparecen una a una, sin conocer cuántas habrá en total? Aquí es donde emerge el desafío. Guardar todas las cartas vistas hasta ahora para seleccionar al final no es viable cuando el flujo puede ser ilimitado o excesivamente grande.
Además, conservar solo una carta y decidir si cambiarla por la siguiente usando solo una moneda al azar puede parecer justo inicialmente, pero como se demuestra matemáticamente, introducirá un sesgo donde las cartas que aparecen más tarde tienen una probabilidad mucho mayor de ser seleccionadas. La esencia de Reservoir Sampling está en ajustar esa probabilidad de forma dinámica con cada nuevo dato recibido. En lugar de un simple cara o cruz, cada nuevo elemento tiene una probabilidad de 1 dividida por el número total de elementos vistos hasta el momento, representado como 1/n, de reemplazar uno de los elementos ya seleccionados. De esta manera, durante las primeras observaciones, cada elemento tiene la oportunidad justa de ingresar al reservorio, y conforme n crece, la probabilidad se ajusta proporcionalmente para preservar la equidad. Esta propiedad se mantiene incluso con la selección de múltiples elementos, modificando la probabilidad de elección a k dividido por n, donde k es la cantidad de espacios disponibles en el reservorio.
Cuando surge la decisión de reemplazar un elemento, se escoge aleatoriamente cuál de los existentes abandonar para dar paso al nuevo. Este mecanismo garantiza que en todo momento los elementos almacenados representan una muestra aleatoria justa de todos los datos vistos hasta ese momento, una característica que se vuelve crucial en aplicaciones prácticas. Una aplicación directa de Reservoir Sampling se encuentra en sistemas de recolección y análisis de logs. En entornos donde servicios generan volúmenes masivos e impredecibles de datos de registro, almacenar o procesar todo podría saturar recursos. En lugar de desechar datos arbitrariamente o limitarse a enviar solo los primeros registros, Reservoir Sampling permite mantener una muestra representativa que se adapta dinámicamente a la cantidad de logs recibidos, garantizando que los datos almacenados sean justos y útiles para futuros análisis sin sobrepasar la capacidad del sistema.
Además, esta técnica optimiza el uso de memoria, dado que siempre se trabaja con una cantidad fija de datos independientes del tamaño del flujo, lo cual es un aspecto vital en la administración de infraestructura tecnológica eficiente y escalable. El algoritmo también permite su implementación sencilla en prácticamente cualquier lenguaje de programación, utilizando estructuras de datos básicas y operaciones matemáticas simples. Aunque Reservoir Sampling es poderoso en su forma básica, existen variantes que abordan necesidades más específicas, como la implementación de versiones ponderadas del muestreo, donde ciertos datos tienen más relevancia que otros y deben tener una probabilidad mayor de selección. Esta extensión abre la puerta a usos más sofisticados en campos como análisis estadístico avanzado, aprendizaje automático y gestión selectiva de datos críticos, aunque su explicación y fórmula son algo más complejas. Reservoir Sampling se revela, entonces, como una técnica indispensable para el tratamiento justo y eficiente de datos en streaming o colecciones desconocidas, combinando elegancia matemática con aplicabilidad práctica.