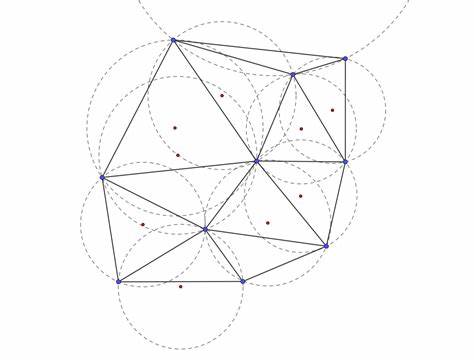
La triangulación de Delaunay es una técnica fundamental en el campo de la geometría computacional que permite dividir un conjunto de puntos en el plano en triángulos de manera que cumplen ciertas propiedades óptimas. Es ampliamente utilizada en áreas que van desde la generación de mallas en gráficos por computadora, pasando por la topografía hasta la creación de redes de comunicación. Su capacidad para maximizar el ángulo mínimo de los triángulos asegura que las formas generadas eviten ángulos agudos y, por ende, mejoran la estabilidad y precisión en numerosos algoritmos y aplicaciones. El procedimiento para realizar una triangulación de Delaunay se basa en la idea de que ningún punto del conjunto debe estar dentro del círculo circunscrito a cualquiera de los triángulos formados. Esto garantiza que los triángulos creados sean lo más equiángulos posible, evitando formas degeneradas que podrían complicar cálculos posteriores.
Para lograr esto, una metodología eficiente y reconocida es la utilización del algoritmo Bowyer-Watson, que permite construir la triangulación de manera incremental y rápida. Una innovación que potencia la velocidad del proceso es el uso del hilbert sort, una técnica que ordena los puntos según una curva de Hilbert, una ruta fractal que visita todos los puntos de una cuadrícula de manera continua y cercana entre sí. Esta ordenación preserva la localización geográfica y facilita que el algoritmo procese primero puntos cercanos entre sí, lo cual reduce considerablemente los tiempos de ejecución. La combinación del hilbert sort con el Bowyer-Watson representa una solución óptima para manejar grandes conjuntos de datos con rapidez y precisión. Más allá de la construcción de triángulos, la triangulación de Delaunay tiene aplicaciones directas en la generación de grafos que reflejan las relaciones entre los puntos.
La estructura resultante puede ser utilizada para construir árboles de mínima expansión, una herramienta clave para optimizar redes, como las de comunicaciones, electricidad o transporte. Al minimizar la suma total de las aristas sin crear ciclos, estos árboles aseguran la eficiencia máxima en la conexión de nodos, facilitando el diseño y análisis de sistemas complejos. La capacidad para renderizar el grafo resultante es igualmente importante. Visualizar los triángulos y las aristas generadas ayuda a detectar patrones, evaluar la distribución espacial y analizar las propiedades geométricas del conjunto. Algunas implementaciones incluyen clases especializadas que permiten representar gráficamente estas estructuras de manera dinámica y clara, potenciando su uso en aplicaciones interactivas y educativas.
Desde el punto de vista computacional, la triangulación de Delaunay es una tarea que puede escalar muy bien si se implementa con los algoritmos adecuados. Los enfoques más básicos pueden caer en una complejidad cuadrática, mientras que técnicas como el hilbert sort combinadas con Bowyer-Watson pueden lograr un rendimiento cercano a O(n log n), que es ideal para manejar grandes cantidades de puntos en tiempo real o en sistemas con recursos limitados. El proceso comienza con un conjunto de puntos distribuidos en el plano, que pueden ser entradas reales de sensores, datos geográficos o cualquier conjunto espacial. El algoritmo crea triángulos que cumplen la condición del círculo vacío, evitando solapamientos incorrectos, y asegurando que las estructuras sean estables para análisis geométricos posteriores. Este proceso no solo tiene ventajas en la precisión sino también en la simplicidad de las estructuras resultantes, que facilitan operaciones como búsquedas, interpolación y generación de mallas.
En sectores donde la simulación y modelado son esenciales, como la ingeniería civil, la meteorología o la informática gráfica, la triangulación de Delaunay se convierte en una herramienta insustituible. Por ejemplo, en la creación de modelos digitales de terreno, permite transformar datos de alturas discretos en superficies continuas y con propiedades matemáticas favorables para cálculos de pendientes, drenajes o visualización en 3D. El impacto en la visualización 3D es particularmente destacado, ya que la triangulación genera una conexión lógica entre puntos que pueden ser utilizados para construir superficies mediante polígonos simples. Esto es esencial para motores gráficos, simulaciones físicas o cualquier entorno que requiera representar el espacio de manera clara y eficiente. Además, la triangulación de Delaunay no solo es importante para puntos en dos dimensiones; sus conceptos y extensiones se aplican en espacios tridimensionales, posibilitando la construcción de tetraedros para aplicaciones complejas como la simulación médica o la exploración geológica.
Aunque la complejidad se aumenta, los principios fundamentales permanecen y continúan garantizando que las estructuras sean óptimas y estables. En la práctica, disponer de una implementación rápida y confiable que combine técnicas avanzadas como el hilbert sort y el algoritmo Bowyer-Watson permite que profesionales de diversas disciplinas puedan integrar esta herramienta en sus sistemas sin sacrificar eficiencia ni precisión. Este tipo de paquetes de software abren la puerta para el desarrollo de soluciones innovadoras, desde planificación urbana hasta análisis de redes inteligentes. Es importante destacar que, si bien el concepto de triangulación de Delaunay es matemáticamente riguroso, su implementación se ha simplificado considerablemente gracias a las librerías modernas y enfoques eficientes. Esto hace que incluso usuarios con conocimientos básicos puedan aprovechar sus beneficios, desde estudiantes que exploran la geometría computacional hasta expertos en análisis espacial.
En conclusión, la triangulación de Delaunay representa una convergencia óptima entre teoría matemática, algoritmos computacionales y aplicaciones prácticas en múltiples campos. Su capacidad para crear estructuras geométricas estables y eficientes permite optimizar tareas complejas, facilitando desde el diseño de grafos y árboles de mínima expansión hasta la visualización de datos espaciales. Su progreso constante y la integración con nuevas tecnologías aseguran que seguirá siendo una herramienta esencial en el escenario tecnológico y científico actual.