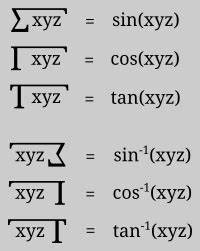La notación trigonométrica de Feynman ha ganado reconocimiento como una herramienta poderosa y creativa para representar funciones trigonométricas y sus transformaciones de una manera simplificada y visualmente atractiva. Esta notación, que toma su nombre del renombrado físico Richard Feynman, ha sido adaptada y extendida para facilitar la enseñanza, comprensión y manipulación de expresiones que involucran funciones trigonométricas. En este contexto, la creación de caracteres personalizados se presenta como un recurso indispensable para quienes buscan presentar información matemática compleja de forma clara y accesible, especialmente en ambientes académicos, científicos y técnicos.</p><p>El origen de la notación trigonométrica de Feynman se basa en el deseo de simplificar la forma en que representamos las relaciones entre funciones trigonométricas, permitiendo una visualización rápida y precisa de sus propiedades y conexiones. Para muchos, las fórmulas tradicionales pueden resultar densas y difíciles de interpretar en etapas iniciales, razón por la que emplear caracteres y símbolos diseñados específicamente para mostrar relaciones específicas puede marcar una gran diferencia en la comprensión del contenido matemático.
El empleo de caracteres personalizados brinda flexibilidad para adecuar la notación al contexto particular de un estudio o proyecto, facilitando la comunicación y el análisis de funciones trigonométricas complejas.</p><p>Crear caracteres personalizados para la notación trigonométrica implica el uso de diferentes herramientas de software, como programas de diseño vectorial, fuentes tipográficas especializadas y sistemas de composición tipográfica avanzados como LaTeX. En el ámbito académico y profesional, LaTeX sigue siendo la plataforma preferida para la elaboración de documentos matemáticos debido a su precisión y capacidad para manejar símbolos personalizados mediante comandos definidos por el usuario. La integración de caracteres personalizados en LaTeX permite no solo mejorar la claridad de las fórmulas sino también estandarizar la presentación en documentos formales.</p><p>Para diseñar un carácter personalizado, es crucial comprender la anatomía de los símbolos trigonométricos y cómo estos se relacionan entre sí.
Por ejemplo, es posible crear variaciones estilísticas de las funciones seno, coseno y tangente que incluyan indicaciones sobre transformaciones específicas, como desplazamientos de fase, ampliaciones o inversiones. Estos caracteres pueden contener elementos gráficos adicionales, como flechas direccionadas, marcadores de ángulo o atributos de color, que faciliten la identificación rápida de las propiedades de la función en cuestión. De esta manera, la notación no solo cumple su función literal, sino que también actúa como un canal visual que transmite información complementaria.</p><p>Además de su aplicación en documentos estáticos, los caracteres personalizados en la notación trigonométrica pueden ser empleados en entornos digitales interactivos. Herramientas como MATLAB, Mathematica o software de visualización matemática avanzada admiten la integración de símbolos personalizados para mejorar la experiencia del usuario al explorar transformaciones trigonométricas en tiempo real.
Estas aplicaciones permiten que estudiantes e investigadores manipulen gráficamente funciones y observen cambios inmediatos en las expresiones, beneficiándose de una comprensión más profunda y dinámica.</p><p>Un aspecto fundamental a considerar al crear caracteres personalizados es la compatibilidad con diferentes dispositivos y plataformas. Para que un símbolo personalizado tenga un impacto real en la comunicación matemática, debe ser accesible y reproducible en diversos entornos, desde computadoras de escritorio hasta dispositivos móviles. Por ello, es recomendable utilizar estándares abiertos y formatos que aseguren la integridad visual de los caracteres independientemente del medio. Asimismo, la documentación y catalogación de estos símbolos personalizados favorece su reutilización y difusión dentro de la comunidad académica y profesional.