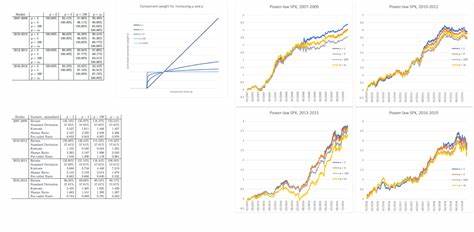
Las leyes de potencia han captado la atención de científicos en diversas disciplinas, desde la biología hasta la física, y su relevancia se extiende a fenómenos que van desde la distribución de las palabras en los idiomas hasta las dinámicas sociales y ecológicas. A medida que los investigadores continúan explorando estas fascinantes relaciones matemáticas, un nuevo conjunto de artículos en la cartera de Nature ofrece perspectivas frescas y valiosas sobre cómo las leyes de potencia influyen en múltiples aspectos de nuestro mundo. En pocas palabras, una ley de potencia describe una relación específica entre dos cantidades, donde una varía como una potencia de la otra. Esto significa que al modificar una de las variables, la otra no sólo cambia, sino que lo hace de una manera que sigue un patrón exponencial. Un ejemplo bien conocido es el principio de Zipf, que establece que la frecuencia de cualquier palabra en un lenguaje es inversamente proporcional a su rango en una tabla de frecuencias.
Así, la palabra más común aparecerá aproximadamente el doble de veces que la segunda más común, y así sucesivamente. Recientemente, en un artículo publicado en Nature Communications, un equipo de investigadores analizó la relación entre la dinámica de la metilación del ADN y la esperanza de vida máxima en mamíferos. Este estudio reveló una relación inversa entre la esperanza de vida y la tasa media de cambios en las regiones de promotores bivalentes del ADN. Los resultados variaron dependiendo del contexto de la cromatina, lo que abre nuevas líneas de investigación sobre cómo los mecanismos epigenéticos pueden influir en la longevidad de los organismos. Este hallazgo no solo es un avance en nuestra comprensión de la biología del envejecimiento, sino que también resalta cómo las leyes de potencia pueden modelar procesos biológicos complejos.
Otro artículo que ha captado la atención de la comunidad científica se centra en las transiciones del estado crítico en la actividad neural bajo el efecto de anestésicos. Los investigadores demostraron que existen múltiples caminos desde una actividad de red autoorganizada (SF) a un comportamiento no SF, sugiriendo que hay una relación compleja entre la actividad neural y el estado de conciencia. Esta investigación no solo es significativa para entender la conciencia y los estados alterados de percepción, sino que también pone de manifiesto la importancia de la teoría de las leyes de potencia para entender sistemas complejos como el cerebro humano. En el campo de la epidemiología, un estudio reciente desarrolló un modelo que anticipa cómo las respuestas conductuales a los riesgos pueden predecir la distribución estadística de los números de infección y reproducción de COVID-19. El análisis se basa en la aplicación de leyes de potencia, mostrando que fenómenos sociales y biológicos pueden ser modelados mediante estas relaciones matemáticas, lo que permite una mejor comprensión de cómo se propagan las enfermedades en las poblaciones.
Además de esos artículos, se han publicado investigaciones que investigan características espectrales generales de la actividad humana y sus fluctuaciones intrínsecas que siguen una ley de 1/f. Este fenómeno, conocido como "ruido 1/f", se ha observado en una variedad de contextos, desde el sonido hasta los mercados financieros, y su presencia en la actividad humana sugiere que nuestra conducta puede estar más entrelazada con patrones naturales de lo que se pensaba anteriormente. Otro hallazgo intrigante en la investigación de leyes de potencia se produjo a raíz de un estudio que analizó la transmisión de enfermedades en ganado. Este estudio identificó parámetros comunes en la transmisión espacial de enfermedades en la ganadería, lo que tiene importantes implicaciones para la salud animal y la agricultura. La capacidad de modelar la propagación de enfermedades en poblaciones de animales mediante leyes de potencia podría ayudar a los veterinarios y a los responsables de salud pública a implementar estrategias más efectivas para controlar brotes.
El debate acerca de si las redes autoorganizadas son raras o universales también ha sido un punto focal en la investigación reciente. Un comentario publicado en Nature Communications argumenta que, a pesar de que algunos investigadores sostienen que estas redes son una excepción más que la norma, hay suficientes evidencias que sugieren la universalidad de los patrones que siguen las leyes de potencia en diversas redes, desde las biológicas hasta las sociales. Tomando en cuenta ajustes en la terminología, el artículo revisita la importancia y el significado de los diseños de red y su relación con la presencia de leyes de potencia. Los artículos en el portafolio de Nature no solo enriquecen nuestra comprensión de las leyes de potencia, sino que iluminan la forma en que estos conceptos matemáticos se manifiestan en el mundo real. Cada nuevo hallazgo ofrece una oportunidad para cuestionar teorías existentes, explorar nuevas preguntas y potencialmente aplicar esta comprensión a problemas prácticos, desde la salud pública hasta la biología del envejecimiento.
Además, el concepto de "adjuntos preferenciales", que describe cómo algunos elementos dentro de una red adquieren más conexiones a medida que aumenta su popularidad o éxito, continúa siendo una temática debatida. Un artículo de opinión publicado en Nature ha reavivado esta discusión, cuestionando si el fenómeno es el resultado de procesos aleatorios o de optimización. Esta controversia no solo es fascinante desde un punto de vista académico, sino que también tiene implicaciones prácticas para la creación y gestión de redes en el mundo moderno. A medida que estos artículos se hacen más accesibles, se hace evidente que el estudio de las leyes de potencia no es únicamente un ejercicio teórico. En un mundo cada vez más complejo, donde las interacciones entre los sistemas biológicos, sociales y tecnológicos son comunes, las leyes de potencia pueden proporcionar un marco valioso para entender y navegar por esa complejidad.
Así, la importancia de las leyes de potencia en el ámbito científico es innegable, y los recientes artículos en Nature son un testimonio de su relevancia y versatilidad. La posibilidad de aplicar conocimientos matemáticos a fenómenos tan diversos nos acerca un poco más a desentrañar los misterios del mundo que nos rodea, revelando patrones ocultos que pueden transformar nuestra forma de pensar y actuar en muchas disciplinas. Con cada nuevo estudio, crece nuestra comprensión de cómo, en última instancia, todo está interconectado en esta vasta red de relaciones que llamamos vida.