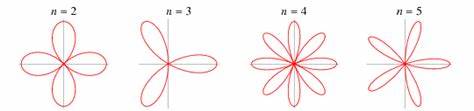
Las rosas, consideradas uno de los símbolos más universales de belleza y delicadeza, ocultan en sus pétalos un misterio que va mucho más allá de su atractivo visual. Detrás de la aparente simplicidad de sus formas se esconde una intricada danza matemática y física que determina las curvas, los bordes y las puntas que hacen que cada pétalo sea único e imprescindible para la identidad de la flor. Los recientes avances científicos han permitido desentrañar el enigma sobre cómo los pétalos de rosa adquieren su forma característica, revelando que un tipo de retroalimentación geométrica nunca antes vista en la naturaleza es responsable de esos contornos puntiagudos y enrollados tan peculiares. Tradicionalmente, la morfología de los pétalos se interpretaba desde un punto de vista biológico, relacionándola con factores genéticos, hormonales y de desarrollo celular. Sin embargo, los estudios emergentes combinan la teoría matemática con la física para ofrecer una nueva perspectiva sobre el crecimiento y la forma.
En particular, investigaciones recientes han demostrado que la forma de los pétalos no es solo fruto de un patrón genético preestablecido, sino también de un proceso autorregulado que responde a la tensión mecánica que surge durante el crecimiento de los tejidos florales. El descubrimiento clave radica en cómo las células en crecimiento generan un estímulo mecánico que, a su vez, regula el ritmo y la dirección del crecimiento, formando un ciclo de retroalimentación mecano-geométrica. Esta dinámica provoca que los pétalos se enrollen hacia afuera y desarrollen bordes irregulares y puntas afiladas. Los físicos han utilizado modelos teóricos y simulaciones por computadora, junto con experimentos con láminas plásticas elásticas que imitan el comportamiento de los tejidos vegetales, para confirmar cómo esta retroalimentación mecánica determina la forma definitiva del pétalo. Este proceso puede compararse con cómo un objeto flexible se deforma bajo tensiones internas: cuando las zonas del pétalo crecen a diferentes ritmos y la estructura responde a estas diferencias con torsiones y curvaturas que minimizan la energía mecánica del sistema.
El resultado es la aparición espontánea de formas complejas sin que exista una programación específica para cada detalle de la forma. En otras palabras, es la interacción entre crecimiento biológico y física geométrica lo que define la elegancia natural del pétalo de rosa. Este fenómeno no solo tiene implicaciones en la comprensión fundamental de la biología del desarrollo, sino que también abre nuevas vías para aplicaciones prácticas. Por ejemplo, entender cómo controlar la morfología mediante la manipulación de las tensiones mecánicas podría inspirar innovaciones en la ingeniería de materiales, diseño de superficies flexibles, e incluso el desarrollo de estructuras autoformativas en robótica blanda. Además, desde una perspectiva botánica, este conocimiento aporta información crucial para la mejora genética y el cultivo de flores, donde la forma no solo es estética sino que afecta la función reproductiva de la planta.
Los experimentos que replican estas mecánicas en laboratorios usan materiales sintéticos que deforman siguiendo patrones similares a los que se observan en las flores. Estas analogías permiten estudiar con gran detalle cómo las irregularidades y puntos agudos emergen de la física subyacente en el crecimiento, algo que sería difícil de observar directamente en organismos vivos. Gracias a la interdisciplinaridad de equipos formados por biólogos, físicos y matemáticos, la investigación sigue avanzando para descubrir qué otras plantas pueden utilizar mecanismos similares y cómo varían estos procesos según el ambiente o la especie. Por otro lado, esta investigación también desafía y enriquece la forma en que se enseña la geometría natural y la biomatemática en la educación científica. Se demuestra que las leyes matemáticas que gobiernan patrones naturales son a menudo no lineales y dependen de variables complejas interconectadas, como tensiones mecánicas generadas por el crecimiento diferencial.
De este modo, el estudio de una flor tan común como la rosa se convierte en un portal para adentrarse en conceptos avanzados de geometría diferencial, mecánica de sólidos y biología del desarrollo. La forma en que los pétalos se curvan y desarrollan bordes acuminados puede también reflejar adaptaciones evolutivas que maximicen la eficiencia en la recepción de luz, la protección frente a daños o la interacción con polinizadores. Por lo tanto, la matemática involucrada no solo es una curiosidad científica sino que tiene un papel funcional en la supervivencia y éxito reproductivo de la planta. Por ejemplo, los bordes puntiagudos pueden facilitar la recogida del rocío o influir en la manera en que la flor se abre según las condiciones climáticas. Profundizando en la teoría, los investigadores han utilizado modelos de crecimiento diferencial incorporando la elasticidad y plasticidad de los tejidos, logrando predecir cómo cambios mínimos en parámetros de crecimiento generan transformaciones drásticas en la forma final.
Esto confirma la sensibilidad del proceso a pequeñas variaciones y sugiere que la diversidad morfológica en la naturaleza puede surgir de estos mecanismos físicos básicos en conjunción con variaciones genéticas. En conclusión, la forma tan característica y hermosa de los pétalos de rosa es el producto de un fenómeno matemático y físico singular, donde el crecimiento, la tensión mecánica y la geometría se entrelazan para producir estructuras complejas y funcionales. Este descubrimiento no solo enriquece nuestra comprensión de la naturaleza sino que ofrece un ejemplo fascinante de cómo la ciencia interdisciplinaria puede revelar los secretos ocultos detrás de la belleza natural. La próxima vez que contemples una rosa, recuerda que cada pétalo lleva consigo el lenguaje oculto de la matemática y la física, una sinfonía estructural que define la perfección en la forma natural.