La distancia de Mahalanobis es un concepto estadístico fundamental que ha revolucionado la forma en que analizamos datos multivariados. Su introducción en 1936 por el estadístico indio P.C. Mahalanobis supuso un avance significativo para la comprensión y comparación de puntos dentro de distribuciones probabilísticas complejas. Hoy en día, se reconoce como una herramienta crucial en campos que van desde la biología y la ecología hasta la economía y la informática.
La capacidad de esta medida para considerar no solo la posición relativa de un punto respecto al centro de los datos, sino también la forma, la dispersión y la correlación entre variables, lo convierte en un método mucho más robusto que la distancia euclidiana tradicional. En esencia, la distancia de Mahalanobis mide cuántas desviaciones estándar multivariadas separan un punto específico del centroide de una distribución. Esto implica que toma en cuenta la matriz de covarianza de los datos, que refleja la variabilidad y las correlaciones entre múltiples variables. Esta característica es especialmente útil en conjuntos de datos donde las variables no son independientes, sino que presentan relaciones complejas entre sí. Comprender cómo funciona la distancia de Mahalanobis puede facilitar la detección de valores atípicos o outliers en contextos multidimensionales, algo que resulta difícil de detectar con simples distancias lineales.
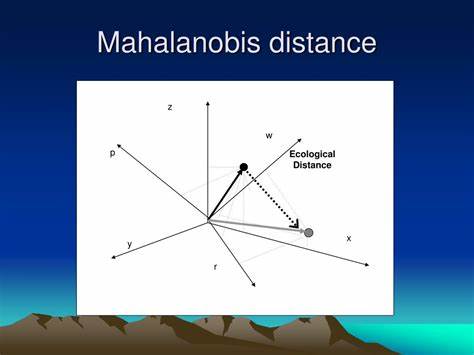
Por ejemplo, en el análisis de datos biométricos, donde múltiples medidas físicas están correlacionadas, esta distancia puede identificar individuos cuyas características difieren significativamente de una población de referencia, considerando la estructura estadística general del grupo. El cálculo se basa en la diferencia entre el vector del punto analizado y el vector de la media de la distribución, multiplicado por el inverso de la matriz de covarianza. Esta operación ponderada ajusta las dimensiones de los datos según su variabilidad, lo que permite interpretar la distancia en términos de la probabilidad de que un dato pertenezca o no a un conjunto determinado. De esta manera, las direcciones con alta varianza permiten mayores desviaciones sin penalización severa, mientras que aquellas con poca variabilidad requieren que el punto esté más cerca para considerarse típico. Una analogía común para explicar la distancia de Mahalanobis es imaginar un conjunto de datos que forman una nube elíptica en un espacio multidimensional.
En esta metáfora, la distancia euclidiana mediria simplemente la distancia recta desde un punto externo al centro, sin importar la orientación o la dispersión de la nube. En cambio, la distancia de Mahalanobis toma en cuenta la forma de esa nube, ajustando la medida para reflejar la verdadera 'proximidad' dentro del contexto del conjunto de datos. Esta metodología es particularmente eficiente cuando los datos siguen una distribución normal multivariada. Bajo esta suposición, la distancia al cuadrado tiene una distribución ji al cuadrado (chi-cuadrado) con grados de libertad iguales al número de dimensiones, permitiendo así establecer umbrales para identificar qué puntos son estadísticamente atípicos o fuera del rango esperado. Además de su papel en la detección de outliers, la distancia de Mahalanobis es fundamental en técnicas de clasificación y clustering.
Por ejemplo, en análisis discriminante de Fisher, se utiliza para asignar muestras desconocidas a grupos basados en su proximidad estadística, maximizando la separación entre clases teniendo en cuenta las covarianzas dentro de cada grupo. De esta forma, se mejora la precisión y la fiabilidad en la clasificación, superando limitaciones de métodos basados solo en distancias directas. Otro uso destacado está en la ecología, específicamente en la modelación del nicho ecológico, donde permite definir el espacio ambiental óptimo para una especie, considerando múltiples factores simultáneamente. Al utilizar la distancia de Mahalanobis, los investigadores pueden construir modelos que reflejen con mayor exactitud las condiciones en las que ciertas especies prosperan, ayudando en la conservación y planificación ambiental. En el ámbito financiero, la distancia de Mahalanobis se emplea para medir la ‘‘turbulencia’’ o cambios anómalos en el comportamiento de mercados financieros.
Este indicador evalúa cómo se desvían las condiciones actuales del mercado respecto a su comportamiento histórico normalizado, proporcionando a analistas y gestores de riesgo una métrica cuantitativa para anticipar periodos de inestabilidad o crisis. Es importante destacar que el cálculo y la aplicación correcta de la distancia de Mahalanobis requieren un manejo adecuado de la matriz de covarianza. En casos donde esta matriz es singular o no es invertible, como cuando existe multicolinealidad o dimensiones superiores a la cantidad de muestras, es necesario aplicar técnicas como la reducción de dimensionalidad o métodos robustos de estimación para obtener resultados válidos. Existen también versiones robustas de la distancia de Mahalanobis que buscan minimizar el impacto de valores extremos o ruido en los datos, tales como el estimador de covarianza mínimo determinante (MCD) o el estimador de elipsoide de volumen mínimo (MVE). Estas variantes fortalecen la resistencia a outliers y mejoran la estabilidad en análisis con datos contaminados.
Desde el punto de vista computacional, esta distancia está bien soportada en múltiples lenguajes y plataformas estadísticas, incluyendo R, Python y MATLAB, facilitando así su integración en pipelines analíticos y software de ciencia de datos. La disponibilidad de funciones optimizadas para su cálculo permite analizar grandes volúmenes de datos sin sacrificar precisión ni velocidad. En resumen, la distancia de Mahalanobis es una herramienta poderosa y versátil que trasciende la simple medición de proximidad. Su capacidad para integrar la estructura de covarianza convierte a esta métrica en una opción ideal para el análisis multivariado, mejorando la detección de anomalías, la clasificación y la modelización en diversos dominios. Comprender y aplicar correctamente esta medida representa una ventaja competitiva para profesionales en estadística, ciencia de datos, ecología, finanzas y más.
La creciente complejidad de los conjuntos de datos modernos exige métodos sofisticados para su análisis. En este contexto, la distancia de Mahalanobis seguirá siendo una referencia indispensable, porque une teoría matemática profunda con aplicaciones prácticas que impactan directamente en la toma de decisiones basada en datos. Adoptarla en las metodologías analíticas es, sin duda, apostar por la precisión y la comprensión en escenarios multidimensionales que de otra forma serían difíciles de interpretar.