El aprendizaje automático se ha convertido en una herramienta indispensable para resolver una gran variedad de problemas, desde la detección de fraudes hasta el diagnóstico médico. Sin embargo, uno de los desafíos más persistentes y complejos es el manejo de conjuntos de datos desbalanceados, donde ciertas clases son mucho más raras que otras. Este desequilibrio puede afectar drásticamente el rendimiento de los modelos, llevando a resultados engañosos si no se trata adecuadamente. En este contexto, un recurso comúnmente utilizado es la técnica de ponderar las clases en proporción inversa a su frecuencia, conocida como peso de clases. Sin embargo, la pregunta es: ¿realmente esta estrategia mejora siempre el rendimiento en problemas con desbalance severo? Y más aún, ¿cómo influye la elección de la métrica de evaluación en la efectividad de estos pesos? Estos son algunos de los puntos que abordaremos en este análisis profundo y fundamentado.
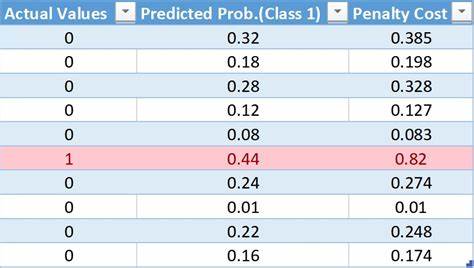
Para comenzar, es importante entender la naturaleza fundamental del problema. Consideremos un escenario típico de clasificación binaria, donde existen dos clases: negativa y positiva. La clase positiva, por ejemplo, podría representar una enfermedad rara en un conjunto de datos médicos, con una prevalencia muy baja – apenas un 1%. Ante esta situación, al construir un modelo que predice si un caso pertenece o no a esta clase positiva, surgen dos tipos principales de error: el falso positivo, cuando se clasifica erróneamente un caso negativo como positivo, y el falso negativo, cuando se omite un caso positivo real. Existe un equilibrio delicado entre estos dos tipos de errores.
Una decisión extrema podría ser simplemente clasificar todos los casos como negativos, lo que elimina completamente los falsos positivos pero resulta en la máxima cantidad de falsos negativos. Por ende, el modelo debe encontrar un compromiso que refleje el costo o la importancia relativa de cada error en el contexto específico del problema. Esta compensación se traduce en la llamada curva de tradeoff entre la sensibilidad y la especificidad del modelo, o entre la tasa de falsos positivos y falsos negativos. Una estrategia común para influir en este equilibrio consiste en asignar un peso diferente a los errores de cada clase durante el entrenamiento, específicamente aumentando el peso de la clase rara para que el modelo preste más atención a esos ejemplos. Conceptualmente, parece lógico pensar que si un modelo se entrena con los errores de la clase positiva multiplicados por un factor mayor, debería mejorar su capacidad para detectar estos casos raros.
Pero la realidad puede ser mucho más compleja. Al analizar matemáticamente la funcionalidad de la pérdida, en particular la entropía cruzada binaria ponderada, se observa que el peso asignado a la clase positiva, denotado por α, determina la posición del modelo en la curva de tradeoff. Esta posición se caracteriza por dos probabilidades: la probabilidad de predecir correctamente un positivo (recall o sensibilidad) y la de predecir correctamente un negativo (especificidad). La relación entre estas probabilidades, así como la prevalencia de la clase positiva (β), condicionan el desempeño esperado del modelo, medido a través de métricas como el F1-score, que combina precisión y recall en un solo valor. Contrario a lo que podría esperarse, investigaciones basadas en modelos teóricos y simulaciones extensas con herramientas prácticas muestran que incrementar α más allá de ciertos valores muy modestos no produce mejoras significativas en el F1-score.
De hecho, utilizar la ponderación típica basada en la inversa de la frecuencia de la clase, que suele ser un valor alto cuando la clase es extremadamente rara, puede incluso perjudicar el desempeño. Este hallazgo desafía la intuición prevalente y plantea que la simple aplicación de pesos proporcionales inversos no es una solución mágica para problemas con desbalance severo. ¿Por qué sucede esto? La explicación radica en cómo el modelo internaliza la relación entre los errores de diferente tipo y cómo se reflejan en métricas específicas. También depende de la naturaleza de la curva de tradeoff que el modelo pueda alcanzar con los datos y las características del problema. Además, la suposición de una curva simétrica entre falsos positivos y falsos negativos es una simplificación que raramente se cumple en entornos reales.
La presencia de ruido en las etiquetas y la calidad de los datos también juegan un papel crucial en la eficacia de la ponderación. Aunado a lo anterior, el impacto de la selección de la métrica de evaluación es fundamental. Mientras que el F1-score pondera la precisión y el recall positivos, muchas guías y tutoriales populares a menudo usan la precisión balanceada o balanced accuracy como métrica principal. Esta métrica calcula el promedio entre la sensibilidad para la clase positiva y la sensibilidad para la clase negativa, otorgando igual importancia a ambas. Al variar el peso de clase y observar la evolución del balanced accuracy, se nota que la ponderación clásica inversa a la frecuencia de la clase sí conduce a un mejor desempeño bajo esta métrica.
En otras palabras, la eficacia del peso de clases está estrechamente atada a la métrica que se pretende optimizar. Para ilustrar la diferencia, imaginemos un conjunto de mil muestras con solo diez casos positivos. Si nuestro modelo predice correctamente las diez positivas (recall positivo del 100%) pero clasifica erróneamente 40 negativos como positivos, la precisión positiva será baja (20%). El balanced accuracy sería alto porque la técnica pondera a partes iguales el recall positivo y el recall negativo, que también es alto. Sin embargo, el F1-score se mantiene bajo debido a la baja precisión, ya que esta métrica refleja con mayor rigor el balance entre falsos positivos y falsos negativos en la clase minoritaria.
Por lo tanto, la elección de la métrica no es solo una cuestión técnica sino estratégica y debe estar alineada con los objetivos del modelo y las prioridades del dominio de aplicación. Esto significa, por ejemplo, que en un contexto médico donde un falso negativo puede costar vidas, podría ser preferible utilizar el F1 o métricas similares que prioricen la detección de la clase rara, mientras que en otros contextos podrían preferirse métricas más balanceadas. Es importante también considerar alternativas a la ponderación de clases, como la calibración del clasificador post-entrenamiento, técnicas de muestreo estratificado, generación de datos sintéticos mediante oversampling o la consideración explícita del costo de errores mediante aprendizaje costo-sensible. Estas opciones pueden complementar o reemplazar la estrategia de peso de clases dependiendo del caso. En resumen, el manejo del desbalance en datasets de clasificación no es una cuestión de aplicar reglas rígidas, sino de comprender profundamente el problema, los costos asociados a cada tipo de error, la forma que toma el compromiso entre precisión y recall y la métrica que se usará para la evaluación final.
La simple aplicación de la ponderación inversa de frecuencia como única solución puede resultar ineficaz o incluso perjudicial. Esta comprensión invita a los científicos de datos y desarrolladores a reflexionar sobre sus pipelines de modelado, asegurar la colaboración estrecha con interesados no técnicos para definir los objetivos y costos reales, y realizar análisis cuidadosos para elegir la estrategia óptima para cada problema particular. El aprendizaje con datos desbalanceados es una aventura que demanda sentido crítico, conocimiento técnico y reflexión constante en cada paso. Finalmente, compartir y actualizar experiencias mediante código abierto y simulaciones reproducibles es esencial para que la comunidad avance con rigor y eficiencia en esta área crítica del aprendizaje automático.