La Forma Más Rápida para Colorear Grafos: Un Avance Revolucionario en Algoritmos

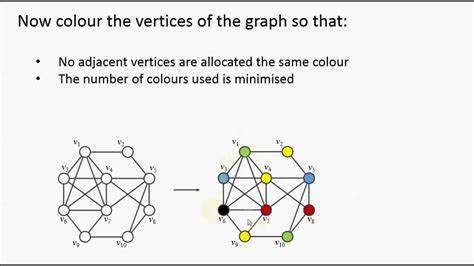
En el dinámico mundo de la informática y las matemáticas, la coloración de grafos representa un problema fundamental con múltiples aplicaciones prácticas, desde la organización del tráfico aéreo hasta la optimización de redes de comunicación. Tradicionalmente, los algoritmos diseñados para asignar colores a las aristas de un grafo han sido lentos, especialmente en grafos grandes y complejos. Sin embargo, recientes avances académicos han logrado romper estas barreras y establecer un nuevo estándar en la eficiencia para colorear grafos. Para entender la importancia de esta mejora, es esencial comprender el problema básico que enfrentan los investigadores: dado un grafo con múltiples puntos (vértices) y conexiones (aristas), ¿cómo coloreamos estas conexiones de manera que ninguna arista que comparta un mismo vértice tenga el mismo color? Este problema es vital para evitar conflictos y solapamientos, como ocurre en escenarios donde diferentes procesos deben compartir recursos sin interferir entre sí. Un ejemplo anodino pero ilustrativo es el control del tráfico aéreo en un aeropuerto concurrido como Newark, cerca de Nueva York.

Visualizando pistas, calles de rodaje y puertas como puntos en un grafo, las rutas de las aeronaves se representan mediante líneas o aristas. Para evitar colisiones y garantizar que dos aviones no estén en el mismo espacio al mismo tiempo, se asignan “colores” a estas rutas que equivalen a franjas horarias. Así, al garantizar que no existan aristas del mismo color convergiendo en un vértice, los controladores evitan conflictos potenciales. Durante décadas, la velocidad de los algoritmos de coloreado de grafos se mantuvo relativamente estancada. En 1964, Vadim Vizing sorprendió al mundo al demostrar que el número mínimo de colores necesarios para colorear un grafo no supera el máximo número de aristas conectadas a un solo vértice más uno.

Este teorema, conocido ahora como el Teorema de Vizing, sentó las bases teóricas para entender el problema. Sin embargo, el verdadero reto no era determinar cuántos colores necesitábamos, sino cómo asignarlos rápidamente a través del grafo. El algoritmo original de Vizing para colorear grafos funcionaba en un tiempo proporcional al producto del número de vértices por el número de aristas. Aunque eficiente para grafos pequeños, en casos con billones de conexiones esta ralentización se volvía impráctica. En las décadas siguientes, varios matemáticos y científicos informáticos intentaron mejorar este rendimiento.

En la década de los 80, aparecieron mejoras notables que redujeron el tiempo de ejecución a valores proporcionales al número de aristas por la raíz cuadrada del número de vértices, pero después de eso, los avances se estancaron. En 2024, la comunidad científica presenció un salto significativo. Sepehr Assadi, junto con su equipo, presentó un algoritmo capaz de reducir el tiempo de coloreado de grafos a un orden basado en el cuadrado del número de vértices, una mejora sustancial en contextos donde los vértices son mucho menos que las aristas. Paralelamente, otro conjunto de investigadores desarrolló una técnica que disminuía el tiempo a una tasa proporcional al producto del número de aristas por la raíz cúbica del número de vértices, refinándose aún más a una proporción con la raíz cuarta. No obstante, ninguno de estos métodos alcanzaba lo que se podría considerar velocidad óptima.

La meta siempre fue clara: lograr un algoritmo en tiempo lineal respecto al número de aristas, porque no se puede colorear un grafo más rápido que el tiempo que se tarda simplemente en leer todas sus conexiones. Esta desafiante meta fue finalmente abordada por un grupo de investigadores que unió fuerzas para ir más allá de mejoras incrementales. Incorporando a Soheil Behnezhad y Martín Costa, este equipo decidió replantear por completo el enfoque tradicional. Mientras todos los intentos previos se centraban en colorear un solo borde rápidamente, estos investigadores optaron por abordar múltiples aristas simultáneamente, cambiando radicalmente el paradigma. Su innovadora estrategia se inspiró en técnicas de pintura de paredes.

Antes de aplicar una capa definitiva de color, los pintores suelen usar una imprimación para preparar la superficie, una técnica que asegura un acabado uniforme y rápido. De manera análoga, los investigadores implementaron un proceso de “priming” aleatorio que preparaba el grafo para el coloreado eficiente. A través de una serie de decisiones aleatorias (similar a lanzar muchas monedas), colorearon gran parte de las aristas de forma rápida y dejaron ciertas partes sin pintar estratégicamente. Estas áreas restantes se pudieron pintar después casi al mismo tiempo sin conflictos. El resultado fue un algoritmo revolucionario que colorea grafos en tiempo cercano al óptimo, específicamente en orden de m log m, donde m es el número de aristas.

Por primera vez, el tiempo de ejecución dependía casi exclusivamente de la cantidad de aristas, independientemente de la cantidad de vértices o la complejidad del grafo. Este avance ha sido reconocido por expertos de renombre como Robert Tarjan, galardonado con el Premio Turing, quien señaló el impacto revolucionario que esta idea de priming ha tenido en el campo. Para muchos, el nuevo algoritmo representa la culminación de décadas de investigación, mostrando que no solo es posible mejorar, sino que algunas barreras simplemente podían ser superadas con una perspectiva fresca y colaborativa. Aunque estos avances son impresionantes en teoría, queda el interrogante sobre su impacto práctico. En aplicaciones reales, los llamados factores constantes — elementos del tiempo de ejecución que no se cuentan en la notación asintótica pero que afectan la velocidad tangible— son cruciales.

Por fortuna, los autores del algoritmo creen que estos factores asociados a su propuesta son pequeños, lo que abre la puerta a posibles implementaciones prácticas en sistemas que requieren decisiones rápidas sobre grafos masivos. Además, la comunidad científica continúa explorando cómo eliminar por completo la dependencia del azar (randomización) en esta técnica, buscando algoritmos deterministas que garanticen siempre el mismo tiempo de ejecución, sin riesgo alguno de ralentizaciones debido a peores casos aleatorios. Por otro lado, también se estudia la posibilidad de suprimir el factor logarítmico que aparece en la ecuación temporal del algoritmo para alcanzar un rendimiento lineal puro, un objetivo técnicamente desafiante que solo ha sido alcanzado en pocas ocasiones para problemas complejos de grafos. La relevancia de estos avances no se limita a la coloración de grafos en sentido estricto. Las mejoras en algoritmos para tratar grandes estructuras de datos tienen repercusiones en campos tan diversos como las telecomunicaciones, inteligencia artificial, algoritmos de optimización y análisis de redes sociales.

Gracias a estos métodos, la gestión eficiente y efectiva de recursos conectados y la prevención de conflictos concurrentes se vuelve una realidad práctica. En conclusión, el panorama de la coloración de grafos ha experimentado un cambio dramático gracias a nuevos algoritmos que combinan ingeniosas ideas aleatorias con técnicas de procesamiento masivo simultáneo. Este avance no solo rompe con décadas de estancamiento, sino que también abre caminos hacia aplicaciones prácticas y desafíos teóricos aún por superar, consolidando un área vibrante y esencial en el núcleo de las ciencias computacionales y matemáticas aplicadas.