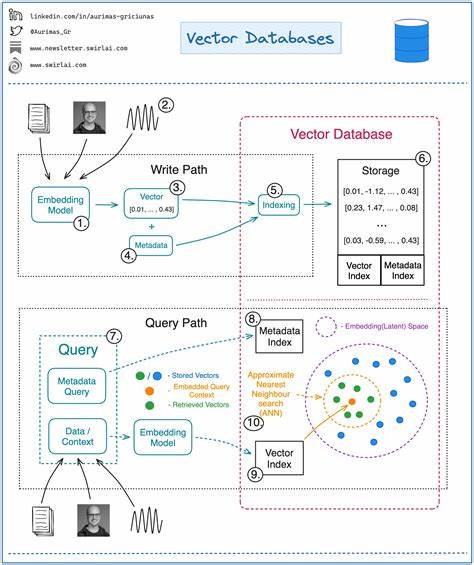
En la era actual de la inteligencia artificial y el aprendizaje automático, el manejo eficiente de datos vectoriales se ha convertido en una pieza clave para aplicaciones como motores de búsqueda, recomendaciones, reconocimiento de imágenes y procesamiento del lenguaje natural. Las bases de datos vectoriales representan un paradigma especializado para almacenar y buscar datos en espacios vectoriales de alta dimensión, permitiendo encontrar los elementos más similares en conjuntos vastos de datos. Para comprender cómo construir una base de datos vectorial propia, es imprescindible entender primero algunos conceptos básicos que sustentan esta tecnología. Un vector es, en esencia, una lista ordenada de números que define una posición en un espacio multidimensional. El número de dimensiones puede variar y las más comunes en aplicaciones actuales oscilan entre 768 y 1536 dimensiones.
Estos vectores representan a partir de modelos de aprendizaje automático, entidades tales como palabras, frases, imágenes o cualquier tipo de información que pueda ser embebida numéricamente para reflejar relaciones semánticas o de similitud. La búsqueda vectorial consiste en encontrar en una gran colección de vectores aquellos que estén más próximos a un vector consulta dado, típicamente midiendo distancias en el espacio, como la distancia euclidiana o la de coseno. Por ejemplo, si un vector representa la frase "Mary tenía un corderito", el sistema debe ser capaz de devolver vectores cercanos que podrían corresponder a frases similares como "Peep tenía una oveja pequeña", incluso si no comparten palabras directamente. Esto es posible gracias a la capacidad del modelo para capturar la semántica y mover vectores similares cerca entre sí en el espacio. No obstante, encontrar los vectores más cercanos a una consulta en una base de datos con millones o miles de millones de elementos es un reto computacional formidable.
No es viable calcular la distancia contra cada elemento individualmente, por lo que es necesario diseñar estructuras y algoritmos eficientes para acelerar estas búsquedas. Un error común al imaginar esta búsqueda es usar analogías de dos dimensiones, como datos geográficos de latitud y longitud. Si pensamos en encontrar propiedades en un mapa, podríamos dividir la superficie en una cuadrícula y buscar dentro de la celda correspondiente a una ubicación dada. Pero esto no es suficiente. Por ejemplo, una cuadrícula muy pequeña puede contener millones de elementos en zonas urbanas densas como Nueva York, mientras que en zonas rurales mucho más grandes, la cuadrícula tendría que ser muy extensa para cubrir la misma proporción de contenido, lo cual es ineficiente.
Este problema se acentúa al aumentar el número de dimensiones, volviéndose la búsqueda intuitiva y las particiones espaciales convencionales menos útiles. La variabilidad en la distribución de los datos, la densidad de las regiones y las dimensiones múltiples requieren métodos más sofisticados para indexar, agrupar y buscar. Una técnica usada para manejar la complejidad es la cuantización de vectores, que simplifica la representación numérica de los datos para ahorrar espacio y tiempo, aunque puede sacrificar algo de precisión. Más avanzado aún es la cuantización de productos (product quantization) y la cuantización binaria mejorada (better binary quantization), que buscan acomodar mejor la distribución real de los datos y preservar la capacidad de búsqueda eficiente. Por ejemplo, en la representación cartográfica, esto sería equivalente a comprimir o expandir ciertas regiones del mapa considerando su densidad poblacional.
Otra línea de trabajo está en el clustering o agrupamiento. Algoritmos como k-means dividen el espacio de datos en grupos o “vecindarios” basados en la proximidad de los vectores entre sí. Esta técnica permite reducir la búsqueda a grupos específicos en lugar de comparar con todo el conjunto, acelerando el proceso y aumentando la precisión. Este método es usado en arquitecturas como los índices invertidos y es fundamental en bases de datos a gran escala como SCANN o SPFresh. Sin embargo, la estructura más influyente y reconocida para grandes bases vectoriales es el uso de grafos, especialmente el modelo Hierarchical Navigable Small Worlds (HNSW).
Este método construye un grafo donde cada nodo representa un vector y está conectado a sus vecinos más cercanos. La búsqueda consiste en recorrer este grafo empezando en un punto de entrada y avanzando hacia nodos cada vez más cercanos al vector consulta. Para evitar ciclos y redundancias, se lleva un registro de los nodos visitados. A nivel técnico, un nodo en este grafo tiene un vector, un identificador y una lista de vecinos. La estructura completa recolecta estos nodos y permite implementar funciones de búsqueda y adición de elementos.
Por ejemplo, durante la búsqueda, se mantiene un heap de nodos ordenados por su distancia al vector consulta, limitando la búsqueda para mantener la eficiencia y sólo acogiendo los k vecinos más cercanos encontrados hasta el momento. El proceso para agregar un nuevo vector en la base consiste en buscar el nodo existente más cercano al vector nuevo y conectar ambos mutuamente. Esta conexión define la topología del grafo y permite que futuras búsquedas aprovechen las conexiones establecidas para llegar rápidamente a vectores relacionados. A pesar de ser una simplificación del HNSW completo, esta aproximación demuestra la eficacia de los grafos para organizar datos en espacios de alta dimensión. Sin embargo, existen consideraciones prácticas imprescindibles para una implementación robusta.
Entre estas se incluyen limitar el número de vecinos por nodo para mantener escalabilidad, conectar cada nodo a múltiples vecinos para mejorar la precisión y abrir la posibilidad de explorar múltiples rutas durante la búsqueda para no perder mejores opciones. El HNSW completo introduce la dimensión jerárquica esencial para la eficiencia en escalas masivas. Al igual que una red vial con calles locales, avenidas, autopistas y carreteras interestatales, la jerarquía permite saltos rápidos a regiones amplias antes de afinar la búsqueda hacia nodos más cercanos. Esto evita recorrer innecesariamente miles de conexiones menores, acelerando el tiempo de respuesta y mejorando la experiencia del usuario. La combinación de los parámetros clave, ef que regula la cantidad de caminos explorados y M que define la conectividad de un nodo, permite ajustar el balance entre velocidad y precisión.
Sin una configuración adecuada, el sistema puede volverse lento o perder calidad en la búsqueda. Dominando estas bases, cualquier desarrollador o investigador puede embarcarse en la creación de su propia base de datos vectorial optimizada para sus necesidades. Estas bases se convierten en el subsistema fundamental para aplicaciones de búsqueda que involucren grandes conjuntos de datos no estructurados, desde sistemas de recomendación hasta motores de búsqueda basados en embeddings de lenguaje natural. El potencial de esta tecnología es inmenso y seguirá creciendo con la evolución de los modelos de inteligencia artificial. Adoptar un enfoque estructurado y entender las técnicas fundamentales es la clave para mantenerse a la vanguardia en la gestión avanzada de datos vectoriales y construir sistemas escalables, precisos y eficientes.
Para quienes deseen profundizar más o experimentar en tiempo real, existen oportunidades para seguir desarrollos y demostraciones en vivo, donde se aborda la implementación práctica y los ajustes finos que hacen posible que estas bases vectoriales sean la columna vertebral de soluciones modernas que impactan desde la industria tecnológica hasta la ciencia de datos avanzada.