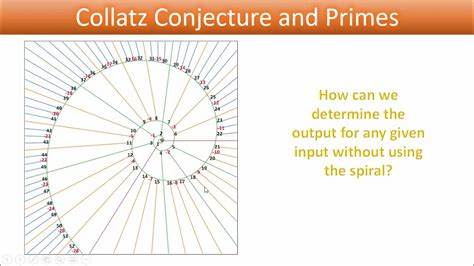
La conjetura de Collatz, también conocida como el problema 3n+1, ha fascinado a matemáticos y científicos durante décadas debido a su aparente simplicidad y complejidad matemática oculta. Consiste en aplicar una operación iterativa a un número entero positivo, donde a cada número impar se le multiplica por tres y se le suma uno antes de dividir por dos, y a cada número par se le divide directamente por dos. El misterio radica en la afirmación no demostrada de que repitiendo este proceso, cualquier número finalmente llegará al ciclo de 1. Pese a ser fácil de entender, la conjetura ha resistido intentos rigurosos de demostración y ha inspirado numerosas aproximaciones teóricas y computacionales. Una de las aportaciones recientes más interesantes es el análisis desde la perspectiva de las factorizaciones primas, lo que permite descubrir una arquitectura matemática que controla el comportamiento de las secuencias generadas.
El análisis de las factorizaciones primas permite simplificar la secuencia original de Collatz, eliminando el llamado “ruido”, es decir, las operaciones innecesarias que oscurecen los patrones reales. Al ajustar el proceso para operar directamente con números impares y considerar la factorización prima del número siguiente par, se identifica un vínculo con la forma en que los números se transforman a lo largo de la iteración. Esto implica visualizar el proceso no sólo en términos de valores individuales, sino a través de la dinámica de sus factores primos, especialmente los números 2 y 3. En particular, el término "número control", definido como c+1 donde c es el número actual en la secuencia, se convierte en la clave para determinar la dirección y longitud de las cadenas ascendentes en el árbol de Collatz. La composición de este número control, en términos de la cantidad de factores primos 2 y 3, revela si la secuencia subirá o bajará y cuántos pasos se tomarán para llegar a un punto límite en la escalada o descenso.
La cantidad combinada de 2s y 3s en la factorización prima indica la extensión de la cadena ascendente, mientras que la presencia exclusiva de 3s marca el límite superior del ascenso. En contraste, la carencia de estos factores sugiere que el número no forma parte de una cadena ascendente. Esta perspectiva permite no solo mapear el camino de cada número en la conjetura sino también entender cómo las diferentes secuencias están interrelacionadas matemáticamente. Los ejemplos prácticos con números concretos ilustran claramente este fenómeno. Por ejemplo, comenzando con el número 15 y observando la factorización del número siguiente 16 (que es 2 a la cuarta potencia), se puede seguir una cadena ascendente donde paulatinamente los factores 2 son reemplazados por factores 3.
Este patrón confirma que el comportamiento de la secuencia Collatz puede interpretarse a través de transformaciones sistemáticas en la composición prima del número. Además, la observación de cómo la conjetura se comporta "en reversa" es especialmente reveladora. El número de factores 3 en la factorización del número control marca cuántos pasos descendentes previos existen, lo que permite reconstruir la trayectoria completa de un número dentro de la secuencia, no sólo hacia adelante sino también hacia atrás. Esto abre la puerta a explorar propiedades estructurales que podrían ser esenciales para una eventual demostración o refutación de la conjetura. Este enfoque también resalta un importante juego matemático entre la transformación de factores primos.
La dinámica de cambiar 2s por 3s y viceversa bajo ciertas condiciones genera cadenas ascendentes y descendentes que nunca se solapan completamente, garantizando que una vez que una secuencia de este tipo cambia de dirección, no regresa a puntos anteriores de la misma manera. Esta característica indica que la conjetura podría ser acíclica, fortaleciendo la hipótesis de que todas las secuencias eventualmente caen al ciclo conocido. La relevancia práctica de investigar la conjetura de Collatz a través de las factorizaciones primas se amplía aún más mediante la implementación computacional. Programas desarrollados para seguir el recorrido optimizado de Collatz e imprimir factorizaciones de números siguientes permiten visualizar y comprender mejor estos patrones. La posibilidad de filtrar ruido y enfocarse en los baches y picos de la serie resalta la estructura subyacente y permite estudiar grandes números con mayor eficiencia.