En el mundo del marketing digital y la analítica de datos, tomar decisiones informadas es fundamental para maximizar el rendimiento y la rentabilidad. Uno de los ejemplos más comunes es cuando una empresa ejecuta una prueba A/B para determinar qué variante de una página web, anuncio o elemento visual genera mejores resultados. Por ejemplo, imagina que tienes un sitio web de comercio y estás decidiendo si mostrar una imagen de un perro o un gato en la página principal. Una prueba A/B revela que la imagen del perro genera, en promedio, más ventas, por lo que parecería lógico simplemente reemplazar la imagen del gato y dar por terminada la prueba. Sin embargo, esta decisión puede ser más compleja de lo que parece a simple vista.
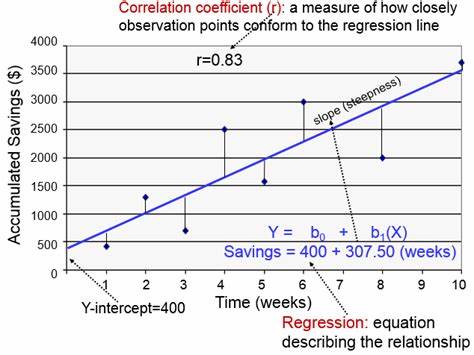
Una estrategia más inteligente consiste en aprovechar la regresión lineal múltiple para personalizar la experiencia del usuario basándose en sus características particulares. En vez de imponer una única variante ganadora para todos, se puede identificar qué usuarios responden mejor a cada opción y adaptar el contenido para aumentar las ventas y la satisfacción del cliente. La regresión lineal múltiple, una técnica estadística con siglos de antigüedad, permite modelar la relación entre una variable dependiente, como las ventas, y múltiples variables independientes, que pueden ser cualquier dato relevante del usuario: navegador web, sistema operativo, ubicación geográfica, entre otros. Este método estima un conjunto de parámetros que indican el efecto individual de cada característica en el resultado final, ajustando automáticamente por la influencia conjunta de todas las demás variables. El corazón matemático de esta técnica se basa en la fórmula beta igual a la inversa del producto de la transpuesta de la matriz X por sí misma, multiplicada por la transpuesta de X y la matriz Y.
Dicho en palabras simples, esta fórmula calcula el conjunto de coeficientes (beta) que mejor describen la relación lineal entre los atributos del usuario y la variable objetivo, utilizando operaciones matriciales como transposición, multiplicación e inversión. Aunque parezca intimidante, cada uno de los pasos necesarios para calcular estos coeficientes puede entenderse como operaciones básicas que los analistas y desarrolladores pueden implementar con relativa facilidad, incluso sin acudir a paquetes estadísticos complejos. El primer paso consiste en computar la matriz que representa todas las combinaciones de categorías y cómo estas se relacionan en la base de datos, algo que puede visualizarse como una tabla dinámica donde se cuenta la coocurrencia entre variables. Un aspecto técnico importante es evitar el problema conocido como la "trampa de variables ficticias" o "dummy trap", que se soluciona eliminando una fila y una columna por cada conjunto de variables categóricas para evitar redundancia y colinealidad. Por ejemplo, si consideramos las plataformas Windows, Mac y Linux, podemos dejar fuera Windows para que actúe como categoría base.
Tras construir esta matriz, el siguiente paso es invertirla. La inversión de matrices es la fase más compleja computacionalmente, pero las librerías numéricas modernas facilitan enormemente esta tarea, permitiendo a los desarrolladores realizarla eficientemente en sus entornos de trabajo, ya sea en C, Python u otros lenguajes con soporte para álgebra lineal. Luego, se calcula otro vector que relaciona las variables independientes con la variable dependiente, en nuestro caso las ventas asociadas a cada característica. Similar a la matriz inicial, este vector se obtiene sumando los valores de ventas por cada segmento específico, cuidando nuevamente de mantener la consistencia eliminando categorías base para evitar duplicidades. Finalmente, la multiplicación de la matriz invertida por este vector da como resultado el vector beta, cuyos valores interpretamos como el impacto estimado de cada característica en las ventas, teniendo en cuenta la influencia combinada de todos los demás factores del modelo.
Por ejemplo, puede que ser un usuario de Mac tenga un efecto positivo en las ventas de cierta imagen, mientras que usar Firefox tenga un efecto negativo, y estos efectos se suman para predecir el resultado esperado para cada usuario. Aplicando este análisis por separado para cada variante del experimento — en este caso, la imagen del gato y la del perro — se pueden obtener dos vectores beta diferentes. Luego, cuando un usuario nuevo visita el sitio, el sistema simplemente evalúa los coeficientes beta correspondientes a sus características para cada variante y predice cuál generará mayor valor esperado, mostrándole la opción óptima de manera automatizada y eficiente. Este enfoque supera la estrategia simple del "ganador absoluto" de las pruebas A/B, usando la información granular recopilada para personalizar en tiempo real las experiencias y maximizar no solo las ventas totales sino también la satisfacción segmentada. En lugar de alienar a los amantes de los gatos por mostrar exclusivamente la imagen del perro, se dirige hacia ellos contenido relevante que resonará mejor con sus preferencias.
Es importante destacar que, aunque los cálculos de la regresión puedan parecer costosos, estos solo necesitan realizarse una vez al final de cada experimento para cada variante, y luego las predicciones en tiempo real son operaciones de muy bajo costo computacional, consistentes en sumas y multiplicaciones sencillas. Esto hace que la regresión lineal múltiple sea muy adecuada para su implementación en entornos de producción con recursos limitados. Además, si se desea asegurar que las diferencias entre las variantes son estadísticamente significativas, es posible realizar pruebas formales como el test de Chow, que evalúa si los vectores beta calculados para cada variante difieren en términos que no sean producto del azar. Para ello, se requiere acceso a funciones estadísticas avanzadas, pero muchas bibliotecas modernas lo facilitan. Los beneficios de integrar modelos de regresión lineal para personalizar decisiones basadas en pruebas A/B son múltiples y van más allá del ejemplo sencillo de imágenes en un sitio web.