La pregunta de cuándo un sistema físico está realizando un cómputo ha sido objeto de debate filosófico, científico y tecnológico durante décadas. A medida que nuevas formas de computación emergen, desde las convencionales hasta las no estándar como la computación cuántica o la biológica, se hace indispensable establecer un marco conceptual que permita distinguir un proceso computacional legítimo de una mera evolución física. En la actualidad, la confusión acerca de qué constituye verdaderamente una computación física es frecuente, tanto por la complejidad de los sistemas como por su representación abstracta. Este análisis se fundamenta en un marco teórico riguroso que aborda la interacción entre niveles abstractos y físicos, la representación matemática y la dinámica del sistema, y culmina con la introducción imprescindible de la figura de la entidad computacional. Al inicio, hay que comprender que la computación es un proceso abstracto definido en términos matemáticos o lógicos.
Por otra parte, un sistema físico es un conjunto tangible de objetos y procesos que evolucionan con el tiempo siguiendo las leyes de la física. El reto consiste en articular el vínculo preciso que gana sentido en la afirmación “el sistema físico X está realizando el cómputo Y”. No basta con observar que cualquier proceso físico puede ser descrito, con suficiente creatividad, por alguna función matemática o algoritmo. De hecho, decir que todo proceso físico es un cómputo se convierte en una trivialidad carente de utilidad. Por ello, la pregunta central es cómo establecer condiciones necesarias y suficientes para identificar una computación física auténtica.
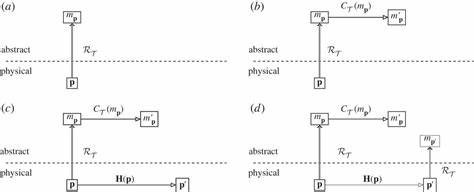
Un punto de partida esencial es la relación de representación. En física, los objetos y sistemas físicos se modelan mediante entidades abstractas: un electrón puede ser representado por una función de onda, un planeta como un punto en un espacio de fases, etc. Esta relación de representación es asimétrica y dependiente del marco teórico: no siempre existe una correspondencia fácil o directa entre un modelo abstracto y un sistema físico, y viceversa. La representación viene dictada no sólo por la naturaleza del sistema sino por la teoría física que utilizamos para describirlo. En la práctica científica, esta dinámica se observa claramente en el proceso experimental: se parte de un sistema físico p, que a través de una representación matemática RT da lugar a un modelo abstracto mp.
Este modelo puede evolucionar en una teoría que predice un estado futuro mp′, mientras que el sistema físico experimenta su propia evolución real a p′. Nuevamente, aplicando la representación se obtiene mp′, el modelo asociado a p′. Un aspecto clave es que el diagrama de evolución sea conmutativo —es decir, mp′ y mp′ deben coincidir o ser suficientemente cercanos— la teoría se considera correcta en su capacidad predictiva. Este mecanismo dual de representación y evolución sustenta también la interpretación de la computación física. La computación, dentro de esta visión, se entiende como el uso intencionado de un sistema físico para obtener la predicción del resultado de una evolución abstracta.
El proceso comienza con un estado abstracto inicial que representa el problema o los datos que se desean computar, el cual debe ser instanciado en un estado físico inicial p mediante la relación de representación inversa o instanciación R~T. Luego, el sistema físico evoluciona y finalmente el estado resultante se representa abstractamente mediante RT para obtener la solución computacional. Es crucial para este proceso que se cuente con una teoría física suficientemente robusta que garantice la coherencia y la confiabilidad en la representación y evolución tanto al principio como al final del proceso. Una de las conexiones más importantes que clarifica el concepto de computación física es la distinción entre computación y mera evolución física. No todo cambio en un sistema físico equivale a un cómputo.
La presencia de codificación y decodificación —representación en ambos extremos— y la existencia de una entidad capaz de llevar a cabo estas operaciones es imprescindible. A esta entidad se la denomina entidad computacional, la cual puede ser humana, biológica, artificial o incluso un dispositivo especializado. Esta figura es responsable de establecer y reconocer la representación de estados abstractos en estados físicos y viceversa. Sin una entidad computacional que otorgue sentido al proceso, la evolución del sistema permanece como un proceso físico sin carácter computacional. Esta perspectiva rescata la objetividad en la definición de computación física.
Aunque pueda parecer que la necesidad de una entidad computacional sugiere subjetividad o dependencia del observador, el marco descrito hace hincapié en que la existencia de encoders y decoders es un hecho físico objetivo dentro del sistema. Como ejemplo, podría observarse a un ser humano usando un calculador: la persona es la entidad computacional, codifica datos en el dispositivo y luego interpreta la salida. Si un gato pulsara al azar las teclas sin entender el proceso, éste no sería la entidad computacional y el proceso no constituiría una computación dirigida sino una mera evolución física accidental. Además, la teoría distingue entre computación y experimentación. En experimentación se realizan observaciones para testear teorías mediante diagramas conmutativos, donde el valor de ϵ —el margen de tolerancia entre predicción y observación— define la validez del modelo.
En computación, sin embargo, es esencial que la predicción abstracta se use para dictar la evolución física, no una descripción a posteriori acomodando datos. Si la interpretación del proceso computacional sólo se realiza post hoc, sin una teoría estable y representación previa, no se puede afirmar que haya habido una computación, sino una simple observación de un fenómeno físico. Las computadoras convencionales, como los dispositivos digitales basados en semiconductores, cumplen a cabalidad con todos estos requisitos. Su arquitectura es ampliamente conocida, las representaciones de estados abstractos a físicos (bits y niveles de voltaje) y viceversa están bien establecidas, y se cuenta con un cuerpo teórico físico que asegura la confiabilidad del proceso computacional. De ahí que puedan usarse para ejecutar algoritmos de manera predecible, con escalabilidad mediante la composición de puertas lógicas.
Por otro lado, los dispositivos de computación no estándar, como los ordenadores cuánticos, sistemas biológicos o dispositivos analógicos complejos, enfrentan retos para demostrar que cumplen estos criterios. Muchas veces, la teoría física que sustenta su comportamiento no está plenamente desarrollada o probada, lo que repercute en la confiabilidad y predictibilidad de sus procesos. Esto genera ambigüedades sobre si están realmente computando o simplemente realizando experimentos físicos complejos que aún no comprendemos del todo. Por ejemplo, controversias en torno a la computación cuántica con máquinas como las desarrolladas por ciertas empresas han puesto en evidencia la dificultad de articular una teoría firme que asegure la correspondencia entre dinámica física y computación abstracta en esos contextos. La computación física también se vincula íntimamente con la simulación, modalidad en la que un sistema físico se usa para predecir el comportamiento de otro sistema físico diferente.
En las simulaciones, es imprescindible un nivel adicional de representación: el sistema simulador debe representar al sistema simulado de manera abstracta y física, estableciendo otro diagrama conmutativo entre ambos. La simulación no es simplemente una computación sino un proceso que combina ambas representaciones y evoluciones. No todos los sistemas físicos simulan a otros, sólo aquellos en los que los procesos de codificación, decodificación y representación están plenamente definidos y validados por la teoría subyacente. En síntesis, la computación física se define como el uso intencionado y basado en una teoría sólida de un sistema físico para llevar a cabo la evolución de un estado abstracto a otro, mediante la codificación en estados físicos y la decodificación posterior. La representación es el eje estructural que conecta lo abstracto con lo físico y recae en las entidades computacionales que otorgan el sentido y estabilidad a este proceso.
Para que un sistema físico compute es indispensable que existan estas condiciones, caso contrario, sólo se estará observando un fenómeno natural, sin la estructura necesaria para ser considerado una computación. Este marco conceptual no sólo aclara un problema filosófico sino que tiene implicaciones prácticas vitales para el desarrollo de futuras tecnologías computacionales. Facilita distinguir usos legítimos de sistemas no estándar como computadores y diferenciar experimentación de computación genuina. A medida que la tecnología avanza y sistemas cada vez más diversos son propuestos para realizar cálculos, la claridad y rigor en la definición de computación física se vuelven herramientas imprescindibles para la innovación responsable y el progreso científico. Finalmente, el reconocimiento de la computación física como un proceso situado en la intersección entre la física, la ingeniería y la matemática fortalece al conocimiento interdisciplinario y redefine a la ciencia de la computación como una ciencia natural.
Al integrar teoría, experimentación, ingeniería y representación, establece un lenguaje común para entender el fenómeno computacional en todo tipo de sistemas, desde los electrónicos tradicionales hasta los más complejos sistemas vivos o mecánicos aún por explorar.