El descenso por gradiente estocástico (SGD) se ha consolidado como uno de los métodos más efectivos para entrenar redes neuronales profundas. Sin embargo, va mucho más allá de ser simplemente un algoritmo para minimizar funciones de costo: posee propiedades inherentes que influyen profundamente en la calidad y generalización de los modelos entrenados. El concepto de regularización implícita en SGD es uno de los avances teóricos más relevantes en los últimos años en el campo del aprendizaje automático. Este fenómeno ayuda a comprender por qué muchas redes profundas, a pesar de ser complejas y capaces de memorizar datos, logran generalizar exitosamente en datos no vistos. Entender el origen y la naturaleza de esta regularización implícita puede transformar la forma en que diseñamos y entrenamos modelos, optimizando su desempeño real en escenarios prácticos.
Para contextualizar el papel de SGD, es fundamental entender que la teoría clásica de la generalización se centró principalmente en las propiedades de la función de pérdida o en la clase del modelo. Sin embargo, en muchos casos, múltiples soluciones a un problema de entrenamiento pueden tener pérdidas prácticamente idénticas en los datos de entrenamiento pero resultar en un desempeño muy distinto cuando se evalúan con datos nuevos. Esto sugiere que el algoritmo de optimización, es decir, la forma en que se recorren y eligen las soluciones, tiene un impacto crucial en el resultado final. En este sentido, la regularización implícita se refiere a la tendencia de los métodos de optimización como el SGD a favorecer ciertos mínimos en la función de pérdida sobre otros, sin necesidad de agregar explícitamente términos de penalización en la función objetivo. Esta preferencia influye en que el modelo converge hacia soluciones con mejor generalización.
Pero ¿cómo se produce esta dinámica y cuál es su fundamento matemático? Para responder esta pregunta, es útil adentrarnos en el análisis diferencial y la teoría de ecuaciones diferenciales, herramientas que han permitido nuevas perspectivas sobre la naturaleza del entrenamiento en redes neuronales. Una técnica particularmente relevante para entender la dinámica de optimización con pasos no infinitesimales es el análisis de error hacia atrás (backward error analysis). Tradicionalmente utilizado en la resolución numérica de ecuaciones diferenciales, este método consiste en identificar un sistema alternativo para el cual la trayectoria discreta generada por un algoritmo de optimización computacional coincide con la solución continua. En el caso del descenso por gradiente, esta perspectiva permite interpretar las iteraciones discretas con paso finito como la evolución continua bajo una función de costo modificada. Esta función ajustada incluye no solo la función original, sino también términos adicionales que actúan como regularizadores implícitos.
Aplicando esta idea a la optimización con gradiente descendiente clásico, se descubre que realizar actualizaciones con un tamaño de paso finito equivale, en el análisis continuo, a introducir una penalización relacionada con la magnitud del gradiente. Es decir, más allá de simplemente minimizar la función de costo, el sistema optimiza un equilibrio entre el valor del costo y la suavidad o estabilidad del gradiente, favoreciendo regiones del espacio paramétrico donde el gradiente es menor, lo que podría interpretarse como una forma de estabilidad inherente del modelo. El análisis se vuelve más complejo y fascinante cuando se aplica al descenso por gradiente estocástico, usado cotidianamente con mini-lotes de datos para acelerar el entrenamiento y aprovechar la variabilidad del muestreo. A diferencia del caso de gradiente completo, donde la trayectoria es determinística, en SGD la dependencia de un muestreo aleatorio induce una distribución de posibles trayectorias que pueden alcanzar diferentes puntos finales. Para abordar esta estocasticidad, los investigadores modelan la evolución media del proceso mediante una ecuación diferencial adaptada, que agrega un término de regularización adicional relacionado con la variabilidad del gradiente en los mini-lotes.
Este término adicional penaliza áreas donde la varianza del gradiente calculado sobre diferentes mini-lotes es alta. Intuitivamente, el algoritmo evita regiones del espacio paramétrico inseguras o inestables en las que pequeñas modificaciones en el subconjunto de datos cambiarían significativamente la dirección del gradiente. Esta propiedad conduce a una selección natural de mínimos donde el modelo es más robusto frente a variaciones en los datos, lo que se vincula directamente con una mejor capacidad de generalización. El impacto fundamental de esta regularización implícita se refleja en que las soluciones a las que convergen SGD y el gradiente completo pueden diferir drásticamente. Aunque ambos métodos buscan minimizar la misma función de pérdida, la adición implícita de términos relacionados con el tamaño del paso y la varianza de gradientes internos afecta profundamente las regiones del espacio que se exploran y los mínimos seleccionados.
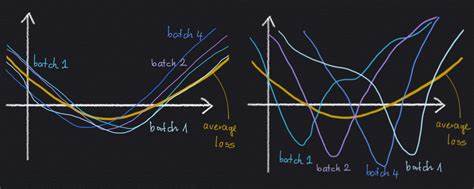
Por ende, SGD no es simplemente un método más rápido para llegar a soluciones similares, sino que induce una dinámica que favorece soluciones de mejor desempeño en datos no vistos. Para ilustrar esta idea, es útil considerar escenarios con múltiples mínimos locales: algunos donde las pérdidas en mini-lotes variados son consistentes y otros en los que existen discrepancias significativas dependiendo del mini-lote evaluado. Los mínimos donde existe concordancia amplia entre mini-lotes suelen ser más anchos y estables, mientras que los que muestran alta variabilidad son más angostos y sensibles a las particularidades del conjunto de entrenamiento utilizado. La regularización implícita en SGD tiende a favorecer la convergencia hacia los primeros, lo que explica en parte por qué modelos complejos entrenados con SGD logran buenos resultados en pruebas. Este descubrimiento también hace evidente cómo la elección de hiperparámetros como la tasa de aprendizaje y el tamaño del mini-lote afectan no solo la velocidad de convergencia sino también el camino de la optimización y, en última instancia, la calidad de la solución.
Por ejemplo, tasas de aprendizaje muy pequeñas o métodos que imitan gradiente continuo clásico pueden perder parte del efecto regulador implícito, mientras que pasos y tamaños de mini-lote cuidadosamente calibrados permiten que la regularización implícita actúe plenamente. Aunque el análisis descrito aporta insights fundamentales, también tiene limitaciones. Por ejemplo, asume que las asignaciones de datos en mini-lotes están fijas y que el azar proviene del orden en que se recorren esos mini-lotes. En la práctica, otras formas de muestreo (como remuestreo con reemplazo) pueden alterar la naturaleza del ruido y por ende la dinámica implícita. Además, la teoría se desarrolla bajo ciertas suposiciones matemáticas que simplifican estructuras reales más complejas de redes y datos.


![Why Perplexity Will Fail [video]](/images/453CEAF2-A72B-431A-8DE7-9D9A66995CE7)