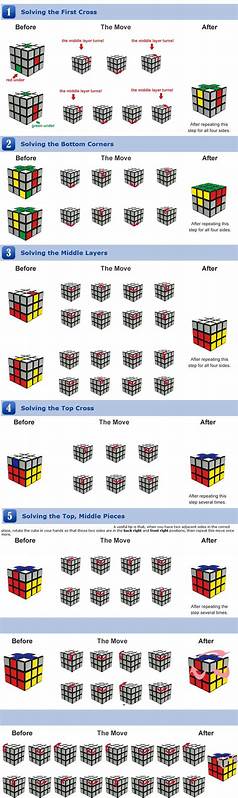
El Cubo de Rubik, inventado en 1974 por Ernő Rubik, se ha convertido en uno de los rompecabezas más icónicos y desafiantes de la historia. Desde su creación, ha capturado la atención no solo de aficionados sino también de matemáticos, científicos de la computación y entusiastas alrededor del mundo. Su complejidad radica en la gran cantidad de posiciones posibles que puede alcanzar: más de 43 trillones. Ante esta vasta cantidad de configuraciones, siempre surgió una pregunta fundamental: ¿cuántos movimientos se necesitan para resolver cualquier posición del Cubo de Rubik? Esta interrogante condujo a un desafío que duró décadas y finalmente, en 2010, fue respondida con un descubrimiento histórico y fundamental para el mundo del cubo y la teoría de grupos: cada posición del Cubo de Rubik puede ser resuelta en 20 movimientos o menos, un número conocido como el Número de Dios (God’s Number). El concepto de God’s Number representa el mínimo número de movimientos que un algoritmo perfecto —o dicho de otra forma, el camino más eficiente— necesitaría para resolver la peor de las situaciones posibles en el Cubo.
En términos simples, es la cantidad máxima de giros necesarios para solucionar cualquier combinación del cubo. Antes de este descubrimiento, había muchos avances que redujeron el rango de movimientos máximos pero sin un número exacto. Por muchos años se sabía que al menos se necesitaban 18 movimientos y el límite superior fue bajando gradualmente desde más de 50 movimientos a medida que investigadores y matemáticos aplicaban nuevos métodos y tecnologías. Entre las posiciones más conocidas está la “Superflip” o super giro, caracterizada por tener todas las aristas volteadas mientras las esquinas permanecen en su lugar. Fue esta configuración la primera en ser probada como un ejemplo que necesitaba 20 movimientos para resolverse, lo cual era un indicio claro de que God’s Number no podía ser menor a 20.
Sin embargo, demostrar que ninguna posición requiriera más de 20 movimientos, es decir, que 20 era tanto el límite inferior como el superior, fue un problema mucho más complejo. Alcanzar esta conclusión demandó el empleo de poderosas herramientas computacionales, técnicas avanzadas en teoría de grupos, simetría y optimización de algoritmos. El equipo detrás de este avance estaba conformado por Tomas Rokicki, Herbert Kociemba, Morley Davidson y John Dethridge, quienes unieron sus conocimientos en programación, matemáticas y computación para enfrentar este desafío. ¿Cómo abordaron un problema que parece imposible de resolver por la enorme cantidad de combinaciones? La estrategia se basó en dividir las más de 43 trillones de posiciones posibles en conjuntos manejables para una computadora actual. Esta fragmentación matemática, conocida como particionamiento en cosets, permitió que cada pieza del rompecabezas -cada subconjunto de posiciones- pudiera ser analizado de manera eficiente usando poderosas técnicas de búsqueda y solución.
Para manejar la complejidad, el equipo también aplicó simetrías del cubo. El Cubo de Rubik posee 24 orientaciones en el espacio, y además incluye simetrías espejadas, lo que reduce el número total de configuraciones distintas que necesitan ser analizadas. Este enfoque permitió disminuir la carga computacional en aproximadamente un factor de 48. A partir de ahí, comenzó la titánica tarea de que miles de computadoras en Google procesaran, en paralelo, los casi 56 millones de conjuntos reducidos. En total, el cálculo requirió alrededor de 35 años de tiempo CPU, pero gracias al poder de la computación distribuida esta monstruosa operación se completó en cuestión de semanas.
Lo más importante es que no fue necesario encontrar la secuencia óptima para cada una de las posiciones, sino simplemente una que resolviera el cubo en 20 movimientos o menos. Este punto fue fundamental para que el proyecto fuera factible en términos de tiempo y recursos. El resultado final se convirtió en un hito en la teoría del cubo y la matemática aplicada: demostraron que ningún estado del Cubo de Rubik puede requerir más de 20 movimientos para resolverse. Esta confirmación cerró un capítulo importante del rompecabezas del Cubo y abrió nuevas puertas en el estudio de algoritmos de optimización y grupos matemáticos. Además del impacto matemático, el descubrimiento tiene implicaciones prácticas para la comunidad cubera.
Muchos algoritmos utilizados por aficionados y profesionales para resolver el cubo suelen requerir más de 40 movimientos, debido a que sus métodos son más simples de memorizar y ejecutar. Saber que siempre existe una solución de 20 movimientos o menos inspira a desarrollar mejores técnicas y programas que ayuden a acercarse a esta eficiencia. También existen numerosas posiciones descubiertas que necesitan exactamente 20 movimientos para resolverse, aunque son extremadamente raras en comparación con la vastísima cantidad de configuraciones posibles. Se estima que hay al menos cientos de millones de posiciones a esta distancia máxima, lo que añade un elemento de misterio y complejidad a la exploración del cubo. Históricamente, esta investigación ha sido una colaboración entre matemáticos, ingenieros y entusiastas del Cubo de Rubik.
Desde Morwen Thistlethwaite en 1981 con su demostración de que 52 movimientos bastan, pasando por sucesivos avances hasta alcanzar el número exacto, el trabajo representa un ejemplo claro de cómo la combinación del trabajo humano con el poder de las computadoras puede resolver problemas aparentemente insuperables. A día de hoy, todavía se continúa explorando variantes del cubo en diferentes métricas de movimientos, como el llamado “quarter turn metric” donde solo se considera cada giro de cara de 90 grados como un movimiento, y cuyo Número de Dios es ligeramente diferente. Por ejemplo, para esta métrica, se sabe que el número máximo necesario para resolver cualquier posición es 26 movimientos. El estudio y perfeccionamiento de algoritmos para resolver el cubo continúa siendo un área activa de investigación, con aplicaciones en la robótica, inteligencia artificial y teoría de la información. En conclusión, la demostración de que cada posición del Cubo de Rubik se puede resolver en 20 movimientos o menos no solo representa la culminación de décadas de trabajo y debate sino también un símbolo del poder de la colaboración interdisciplinaria y tecnológica.
Este hito no solo satisface la curiosidad de fanáticos y expertos sino que también estimula la innovación en múltiples áreas de la ciencia y tecnología. Gracias a la combinación de matemáticas avanzadas, computación distribuida y técnicas de optimización, hoy conocemos el límite exacto para resolver uno de los rompecabezas más emblemáticos de la historia humana.