El sistema francés de amortización de préstamos es uno de los métodos más utilizados a nivel mundial para estructurar el pago de hipotecas y otros tipos de créditos a tasa fija. Aunque muchas personas escuchan comúnmente que al principio se pagan más intereses y luego una mayor parte del pago se destina a amortizar el capital, pocas entienden el fundamento matemático y financiero que sustenta este esquema. Comprender cómo funciona este modelo no solo ayuda a planificar mejor las finanzas personales sino también brinda una visión clara de cómo evoluciona la deuda a lo largo del tiempo. Cuando se obtiene un préstamo, ya sea hipotecario u otro, con una tasa fija de interés, el prestatario realiza pagos mensuales constantes que dependen de tres variables clave: el monto total del préstamo, la tasa de interés periódica y el número total de pagos que se harán hasta liquidar la deuda. Estos tres factores permiten calcular un monto fijo mensual mediante una fórmula matemática específica que determina el pago exacto para ir amortizando el capital e intereses durante el plazo acordado.
La fórmula que sirve para calcular estos pagos mensuales es: PMT = P × [r(1+r)^n] / [(1+r)^n − 1], donde PMT representa el pago mensual, P es el principal o monto del préstamo, r es la tasa de interés periódica (en el caso de pagos mensuales será la tasa anual dividida entre 12) y n el número total de pagos. Esta ecuación resulta en un pago fijo mensual que cubre la porción de intereses y capital correspondientes a cada periodo. Para ilustrar su funcionamiento supongamos que se obtiene un préstamo hipotecario de 100.000 euros con una tasa fija anual de 3,5% y se planea pagar en 25 años. En primer lugar se calculará la tasa mensual dividiendo la tasa anual entre 12, lo que genera aproximadamente 0,00292 o 0,292% mensual.
Luego, multiplicando los años por la cantidad de meses, se determinan 300 pagos en total. Aplicando la fórmula matemática, el pago mensual resultante es cercano a 500,84 euros. Entender que cada pago mensual no se destina únicamente a reducir el capital es fundamental. Al inicio del préstamo, la mayoría del pago cubre los intereses generados por la deuda pendiente. Por ejemplo, en el primer mes el interés será el saldo inicial multiplicado por la tasa mensual, lo que da aproximadamente 292 euros.
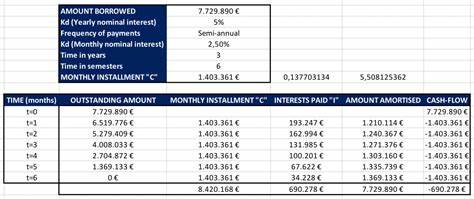
La diferencia entre el pago total y el interés corresponde a la parte que reduce el capital, es decir, unos 208,84 euros. Al mes siguiente el saldo para calcular intereses será menor porque se ha reducido el capital y, en consecuencia, la parte que va a intereses es menor y la que paga capital es mayor. Este proceso continúa mes a mes incrementando la proporción del pago destinada a amortizar el capital y disminuyendo la que corresponde a intereses, lo que finalmente termina en la liquidación completa del préstamo. Este modelo establece un equilibrio financiero que facilita la previsión de pagos y su impacto en las finanzas personales. Este mecanismo se puede visualizar perfectamente en una tabla de amortización que desglosa mes a mes el monto del pago, cuánto de ese pago es interés, cuánto reembolsa capital y cuál es el saldo restante del préstamo.
Al analizar dicha tabla se observa que con cada abono mensual la deuda pendiente disminuye, haciendo que los intereses para el siguiente pago sean menores. De este modo, el capital se amortiza progresivamente mientras los intereses decrecen. Desde una perspectiva matemática y financiera, este método no es arbitrario. De hecho, el sistema francés de amortización es una aplicación directa del método de flujo de caja descontado utilizado para valorar inversiones. El banco o entidad financiera que otorga el préstamo realiza una inversión - entregando un capital hoy - y espera recibir una serie de flujos de caja futuros representados por los pagos mensuales efectuados por el cliente.
El valor presente de esos flujos de caja descontados a la tasa pactada debería coincidir con el monto inicial del préstamo. El cálculo del valor presente se hace mediante la suma de los pagos futuros descontados en función de la tasa de interés periódica para reflejar el valor real hoy. Esta técnica permite establecer claramente lo que debe pagarse en cada periodo para que la entidad financiera cobre exactamente lo que prestó más los intereses acordados durante la vida del crédito. Si se replantea la fórmula original del pago mensual se puede obtener su forma cerrada a partir de la ecuación del valor presente. Mediante herramientas matemáticas como las progresiones geométricas y algebraicas se encuentra una expresión que permite despejar el pago mensual a partir del monto prestado, la tasa y la duración del préstamo sin necesidad de realizar sumatorias prolongadas para cada caso.
Automatizar el cálculo del cronograma de amortización es hoy en día posible gracias a programas y lenguajes de programación como Python, que facilitan la construcción de tablas que muestran mes a mes el pago, porcentaje destinado a intereses y al capital, y el saldo remanente. Además, existen librerías especializadas como numpy-financial que mediante funciones específicas pueden obtener el pago mensual fijo y fraccionar automáticamente cada pago en seguros incrementos de interés y amortización según corresponda. Entender el sistema francés de amortización es esencial para todos aquellos que planean adquirir una vivienda mediante hipoteca o contraer cualquier tipo de préstamo a largo plazo. Les permite calcular anticipadamente cuánto van a pagar y cómo evolucionará la deuda, ayudando a mejorar la gestión financiera y tomar decisiones más informadas. Asimismo, comprender que al inicio los intereses absorben la mayor parte del pago y que sólo con el tiempo se empieza a reducir significativamente el capital puede fomentar prácticas responsables como realizar pagos anticipados o renegociar condiciones cuando sea posible.
En esencia, el método francés representa una forma equilibrada y matemática de dividir y planificar el pago de una deuda que genera seguridad y previsibilidad tanto para el crédito como para el deudor. A través de este sistema se consigue un proceso gradual de construcción de patrimonio al reducir el capital pendiente, y a la vez se garantiza a la entidad financiera la recepción constante de sus intereses estipulados, siendo un pilar fundamental en el mercado hipotecario y financiero global.