En el mundo de la investigación operativa y la inteligencia artificial, la resolución de problemas complejos con múltiples restricciones es un desafío constante. Algunos problemas se vuelven incluso más intrincados cuando resultan ser infeasibles debido a restricciones contradictorias o inconsistentes. Frente a esta dificultad, surge una solución innovadora que combina redes neuronales de grafos (GNN) y aprendizaje por refuerzo profundo (DRL) para reparar automáticamente estos problemas y restaurar su viabilidad. Este enfoque, desarrollado recientemente en un proyecto de vanguardia, no solo abre nuevas puertas en la automatización de la identificación y corrección de problemas infeasibles, sino que también redefine la forma en que los sistemas inteligentes abordan problemas complejos en dominios lineales y booleanos. Los problemas de satisfacción de restricciones (CSP, por sus siglas en inglés) se presentan comúnmente en muchas aplicaciones, desde la optimización logística hasta la planificación y programación avanzada.
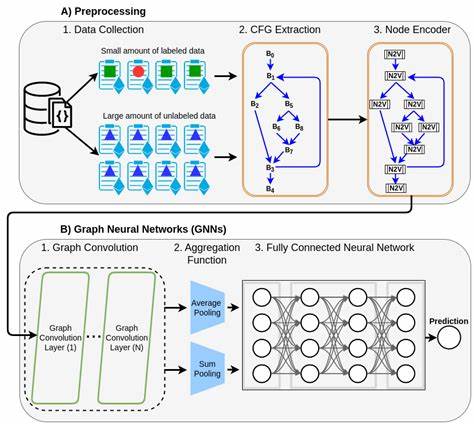
Cuando estos problemas se vuelven infranqueables por imposibilidades internas originadas en las restricciones, la dificultad radica en identificar qué restricciones ajustar o eliminar para restaurar la factibilidad sin perder la esencia o el objetivo del problema. Tradicionalmente, esto requería intervención humana experta y análisis manual extenso, pero la introducción del aprendizaje profundo y las representaciones basadas en grafos ha proporcionado soluciones inteligentes y automatizadas. El núcleo del método radica en representar los problemas de satisfacción de restricciones como grafos bipartitos, donde un conjunto de nodos representa las variables y otro las restricciones. Esta estructuración facilita la captura de las interacciones complejas y dependencias entre distintas restricciones y variables. A partir de esta representación, se implementan redes neuronales de grafos, que a través de un proceso iterativo llamado “message passing” o propagación de mensajes, actualizan las representaciones internas de los nodos del grafo, permitiendo al sistema entender la complejidad y dinámica del problema completo.
El aprendizaje por refuerzo profundo complementa esta capacidad al transformar el problema de reparación en un proceso de toma de decisiones secuencial modelado como un proceso de decisión de Markov (MDP). En este contexto, un agente inteligente debe aprender una política óptima para seleccionar cuál restricción eliminar en cada paso con el fin de alcanzar la factibilidad con el mínimo ajuste posible. Para entrenar al agente, se utiliza un algoritmo avanzado de aprendizaje por refuerzo como Proximal Policy Optimization (PPO), reconocido por su eficiencia y estabilidad en entornos complejos. El entrenamiento y evaluación de la solución demuestran su robustez y eficiencia tanto en problemas conocidos de optimización lineal como en problemas booleanos de satisfacibilidad (SAT). Este enfoque no solo repara problemas dañados, sino que también establece una base para el análisis automático de la causa raíz de infeasibilidades, una tarea hasta ahora poco explorada desde la óptica del aprendizaje profundo.
Uno de los aspectos más destacados es la formalización del problema de reparación de un CSP como un problema de camino más corto en grafos. Esto implica que la solución óptima corresponde a encontrar el conjunto mínimo de restricciones cuyo ajuste—típicamente la eliminación—permite que el problema se vuelva compatible. Esta perspectiva abre la posibilidad de aplicar diversas herramientas clásicas y modernas de teoría de grafos y optimización combinatoria al dominio de la inteligencia artificial y el aprendizaje automático. Además de su base teórica sólida, este proyecto proporciona un marco práctico y accesible mediante un repositorio abierto en GitHub. En él, la comunidad puede encontrar código, ejemplos y configuraciones listas para ejecutar experimentos propios.
La flexibilidad del código permite aplicar la metodología a distintos tipos de problemas y ajustar arquitecturas de redes neuronales y parámetros del entorno para adaptarse a diversos escenarios reales. El impacto potencial de esta técnica es amplio y significativo. En áreas como la logística, programación de recursos y diseño de sistemas complejos, la capacidad de detectar automáticamente problemas de factibilidad y aplicar reparaciones inteligentes puede reducir costos, tiempos y riesgos asociados a fallas o inconsistencias. Además, el enfoque representa un avance en la integración entre aprendizaje automático y métodos clásicos de investigación operativa, demostrando cómo la combinación interdisciplinaria puede superar limitaciones tradicionales. Este proyecto también marca un hito en la investigación aplicada al demostrar que el aprendizaje por refuerzo no solo puede ser usado para solucionar directamente problemas complejos sino también para reparar y mejorar instancias problemáticas mediante decisiones informadas.