¿Por Qué No Deberías Invertir una Matriz Para Resolver Ax = b? Descubre las Razones Fundamentales

En el mundo del álgebra lineal numérica, un consejo recurrente y hasta cierto punto dogmático es evitar la inversión directa de matrices para resolver sistemas lineales de la forma Ax = b. Pero, ¿por qué sucede esto? A primera vista, podría parecer lógico obtener el vector incógnita x multiplicando el vector b por la inversa de A, es decir, x = A⁻¹b. No obstante, esta práctica suele ser ineficiente y puede conllevar problemas de precisión numérica que merecen una explicación detallada. El núcleo del problema radica en que el proceso de invertir una matriz completa es mucho más costoso computacionalmente y más propenso a errores acumulados que otras estrategias más sofisticadas para resolver ecuaciones lineales. Uno de los métodos más comunes y efectivos es la descomposición LU, que forma parte del grupo de técnicas que transforman una matriz original en otras con propiedades especiales que facilitan la resolución del sistema sin necesidad de calcular la inversa.

Desglosemos primero qué es la descomposición LU. Consiste en factorizar una matriz A en el producto de dos matrices: una triangular inferior L y otra triangular superior U. Esto se logra aplicando transformaciones lineales secuenciales que, en esencia, van introduciendo ceros sistemáticamente en la matriz original para facilitar el cálculo. Gracias a la estructura triangular de estas matrices, resolver sistemas como Ly = b y posteriormente Ux = y es mucho más simple, directo y con un menor costo computacional. Desde la perspectiva del costo de cómputo, calcular una inversa conlleva realizar aproximadamente más del triple de operaciones aritméticas (flops) que resolver un sistema mediante descomposición LU y sustituciones sucesivas.

Además, la multiplicación de la inversa calculada por el vector b también añade operaciones adicionales, incrementando aún más el tiempo de procesamiento y la posibilidad de acumulación de errores numéricos. Pero el costo no es la única desventaja. Desde el punto de vista numérico, invertir una matriz puede amplificar los errores existentes en los datos o errores de redondeo inherentes a la aritmética de punto flotante usada en los ordenadores. Esto es especialmente crítico cuando la matriz A está mal condicionada, es decir, cuando su número de condición es grande. El número de condición es una medida que indica qué tan sensible es la solución del sistema lineal a cambios o errores en la matriz A o en los datos b.

Matemáticamente, el número de condición está definido como el producto de la norma de la matriz A por la norma de su inversa. Altos valores de este número indican que la matriz es cercana a ser singular o que posee singularidades que hacen que la solución sea inestable o altamente sensible a pequeñas perturbaciones. Cuando la matriz es mal condicionada, los errores producidos al invertirla y posteriormente multiplicar por b suelen ser bastante mayores que los que se obtienen al resolver directamente el sistema mediante descomposición LU y sustituciones. Por lo tanto, la solución obtendida mediante la inversión suele tener un error residual más alto y es menos confiable. Esto no quiere decir que invertir matrices sea una práctica siempre inapropiada en cualquier contexto.

Existen situaciones específicas donde, por ejemplo, la inversa de una matriz necesita ser reutilizada para múltiples resoluciones con diferentes vectores b o para otros análisis matemáticos. Sin embargo, para la mayoría de aplicaciones donde simplemente se busca resolver Ax = b una vez, la recomendación es clara: no se debe invertir la matriz. Además, los software matemáticos modernos y las librerías de álgebra lineal implementan métodos optimizados para resolver sistemas de ecuaciones que aprovechan estas técnicas, evitando explícitamente el cálculo de la inversa. Funciones como numpy.linalg.

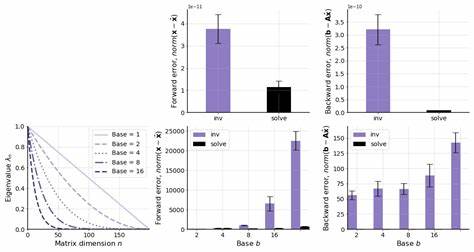
solve en Python o similares en Matlab y Julia, usan internamente estrategias como la descomposición LU o QR para brindar resultados más rápidos y confiables. A modo de ejemplo numérico, si se considera una matriz de tamaño n por n, el proceso de descomposición LU y la posterior resolución del sistema tiene una complejidad de aproximadamente (2/3)n³ operaciones flotantes, mientras que la inversión de la matriz y la multiplicación por un vector b puede llegar a implicar cerca de 3n³ flops, lo cual es considerablemente superior. Por su parte, el concepto de forward y backward error complementa esta explicación. La diferencia entre la solución computada y la solución exacta es el error hacia adelante, mientras que el error hacia atrás mide cuánto deberían cambiar los datos de entrada para obtener la solución computada como exacta. En la mayoría de las aplicaciones prácticas, minimizar el error hacia atrás es fundamental para garantizar estabilidad y confiabilidad.

Las soluciones obtenidas mediante resolución directa del sistema mantienen en general un bajo error hacia atrás. En cambio, la inversión directa puede ocasionar un error hacia atrás sustancialmente mayor, degradando la calidad de la solución principalmente cuando la matriz es mal condicionada. Investigaciones y experimentos recientes han evidenciado que en condiciones bien condicionadas, la diferencia entre usar la inversa o la resolución directa puede ser menos dramática en términos de error hacia adelante. Sin embargo, la forma más segura, eficiente y adoptada universalmente sigue siendo la resolución directa de sistemas mediante técnicas como LU, evitando la menos deseada inversión explícita. En conclusión, invertir una matriz para resolver Ax = b no solo es una operación computacionalmente costosa sino que además puede introducir errores significativos que afectan la exactitud y estabilidad de la solución.

Métodos basados en descomposiciones y sustituciones triangulares no solo son más rápidos sino que también contribuyen a obtener soluciones más estables y confiables en la mayoría de escenarios prácticos. Por tanto, como regla general en álgebra lineal computacional, es recomendable siempre optar por la resolución directa de sistemas lineales y evitar la tentación de calcular directamente la inversa de una matriz salvo que se justifique explícitamente su necesidad por el problema en cuestión. Esta práctica mejora la eficiencia, reduce los errores numéricos y permite utilizar los recursos computacionales de forma más inteligente, especialmente en problemas de gran escala o en aplicaciones donde la precisión es crítica. Por ello, al enfrentar la ecuación Ax = b, recuerda: resolver directamente, no invertir.