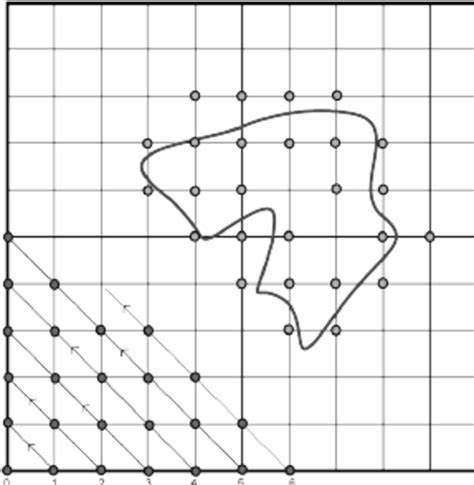
Las funciones de distancia signadas, conocidas comúnmente como SDFs por sus siglas en inglés, y el algoritmo de barrido rápido son conceptos fundamentales en el análisis numérico y la simulación computacional, con usos que abarcan desde la representación implícita de superficies hasta la modelización de ondas y la evolución de interfaces. La combinación de estos elementos con JAX, la biblioteca de Python que permite el cálculo numérico acelerado y diferenciado, está revolucionando la forma en que se implementan y optimizan métodos numéricos. En este texto, exploraremos a profundidad los principios detrás de las SDFs, el significado físico y matemático de la ecuación de Eikonal, y cómo el algoritmo de barrido rápido se utiliza eficazmente para resolver esta ecuación, destacando una implementación específica en JAX que ofrece ventajas notables en velocidad y optimización. Las funciones de distancia signadas son herramientas que permiten describir de forma implícita la forma y posición de un objeto dentro de un espacio, generalmente n-dimensional. Estas funciones proporcionan la distancia mínima desde cualquier punto del espacio hasta la frontera del objeto, asignando un signo para indicar si el punto está dentro o fuera del objeto.
Esta manera de representar superficies es sumamente útil porque permite describir interfaces complejas sin necesidad de seguir explícitamente todos sus puntos o mallas, lo que sería costoso y complicado en términos computacionales. Las SDFs son esenciales en la estrategia conocida como método de nivel set, donde la frontera de interés se representa como el conjunto de puntos en que la función toma el valor cero, permitiendo rastrear la evolución de estas fronteras mediante el cálculo de la función en un dominio fijo y discreto. El método de nivel set es, en esencia, una estrategia euleriana para la simulación de interfaces en lugar de un enfoque lagrangiano. Esto significa que en lugar de seguir el movimiento individual de puntos que definen una superficie (como partículas en la frontera), se define una función escalar sobre un dominio fijo en el espacio, y la frontera emerge automáticamente donde la función toma valor nulo. Esta representación es ventajosa principalmente porque puede manejar cambios topológicos complejos, como la fusión o división de superficies, sin requerir una reconfiguración explícita de la malla o conjunto de puntos.
El núcleo matemático para la evolución de la función nivel set está dictado por la ecuación de Eikonal, un tipo de ecuación en derivadas parciales hiperbólica que describe la propagación de frentes a velocidad dada. Formalmente, la ecuación se expresa como el producto entre la magnitud del gradiente de la función de llegada o tiempo, “∇T”, y la velocidad local “F”, igual a uno. En términos intuitivos, esta ecuación modela fenómenos como la propagación de ondas, la difusión de un fuego o la progresión de un frente de inundación. El valor “T” en un punto específico representa el tiempo en el que el frente llega a esa posición, mientras que “F” define la rapidez con la que dicho frente se propaga en ese punto. Resolver la ecuación de Eikonal es fundamental para obtener la función de distancia signada, especialmente cuando la velocidad “F” es constante o igual a uno.
Sin embargo, esta ecuación presenta desafíos numéricos, ya que puede desarrollar discontinuidades y singularidades en la solución, particularmente cerca de obstáculos o configuraciones complejas de la interfaz. Estos fenómenos, denominados “shocks”, dificultan el uso de métodos numéricos clásicos que dependen de aproximaciones continuas y suaves. Por ello, se han desarrollado algoritmos especializados que pueden manejar este tipo de irregularidades. El método de barrido rápido es un algoritmo numérico diseñado para resolver la ecuación de Eikonal de manera eficiente en dominios discretizados. A diferencia del método de marching rápido, que utiliza estructuras de datos complejas para resolver el problema en tiempo logarítmico respecto al tamaño de la malla, el método de barrido rápido aprovecha una serie de barridos sobre la malla en diferentes direcciones para propagar la información de llegada desde la frontera inicial hacia el resto del dominio, ofreciendo una complejidad lineal en el número de nodos.
Esta propiedad lineal hace que sea extremadamente atractivo para problemas grandes o de alta resolución. El algoritmo realiza estos barridos cubriendo todas las combinaciones posibles de las direcciones espaciales, asegurando que la información se actualice progresivamente desde distintos “cuadrantes” o direcciones, respetando el principio de upwinding o diferencias ascendentales, que garantiza que la información fluya correctamente en la dirección del frente. En cada paso, el algoritmo resuelve una formulación local de la ecuación de Eikonal a través de la solución explícita de una ecuación cuadrática, actualizando el valor de llegada en el punto actual si encuentra un valor menor al registrado previamente. Implementar el método de barrido rápido en frameworks tradicionales puede ser lento o poco eficiente debido a las dependencias en bucles y actualizaciones secuenciales, pero con JAX, es posible aprovechar la compilación just-in-time, la optimización automática y la paralelización sobre CPU y GPU para acelerar significativamente esta tarea. JAX, al estar basado en transformaciones funcionales y sus propios mecanismos de trazado y compilación, permite expresar el algoritmo en un estilo funcional y declarativo que resulta al mismo tiempo elegante y altamente performante.
Un ejemplo de implementación en JAX del método de barrido rápido comienza por definir las cuatro direcciones de barrido en dos dimensiones (de arriba a abajo y derecha a izquierda, entre otras combinaciones). A cada iteración, el algoritmo realiza un barrido para actualizar el campo de llegada, ignorando aquellas células que corresponden a la frontera fija o a obstáculos definidos, que se consideran “frozadas” y no cambian durante la simulación. Durante cada barrido, para cada celda que no esté congelada, se calcula una actualización local empleando valores de vecino inmediatos y se usa la solución de la ecuación cuadrática para reestimar el tiempo de llegada. Estas actualizaciones se van combinando para refinar cada vez más la estimación global. El proceso se itera varias veces, garantizando la convergencia de la solución.
Este enfoque no solo es intuitivo sino que también es altamente adaptable, ya que permite incorporar obstáculos y condiciones iniciales complejas fácilmente, solo modificando las matrices de máscara correspondientes, sin cambiar la estructura del algoritmo central. Además, la habilidad de JAX para integrar funciones definidas en Python con operaciones vectorizadas hace posible mantener un equilibrio óptimo entre legibilidad y rendimiento. El uso del método combinado de SDF y fast sweeping en JAX tiene aplicaciones prácticas que van desde la simulación física, la robótica y el análisis geofísico, hasta la reconstrucción implícita en machine learning, donde se trabaja con formas tridimensionales complejas y su evolución temporal. Por ejemplo, en reconstrucción 3D, la obtención rápida y precisa de funciones de distancia permite mejorar algoritmos de rendering o detección de colisiones. Aunque existen métodos alternativos para resolver la ecuación de Eikonal, como el método de marching rápido o técnicas basadas en Runge-Kutta para PDEs, estos suelen ser más lentos o menos estables en problemas con geometrías complicadas o con presencia de singularidades.
Por esta razón, el método de barrido rápido se presenta como una opción sólida, y, cuando se implementa con herramientas modernas como JAX, ofrece la velocidad necesaria para trabajar con datos voluminosos o en tiempo real. En cuanto a la paralelización del método de barrido rápido, es un tópico interesante y activo dentro de la comunidad científica. En teoría, los barridos en diferentes direcciones podrían ejecutarse en paralelo y luego combinarse al tomar el mínimo elemento a elemento. Sin embargo, implementar esto de forma eficiente en entornos como JAX resulta retador por la forma en que el trazado computacional controla el flujo y la estructura dinámica del código. Encontrar una forma práctica y eficiente de paralelizar estos barridos sin perder estabilidad o precisión es un área de investigación vigente.